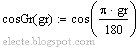Электротехника: 2011

суббота, 31 декабря 2011 г.

Светодиодная мигалка.

Схема мигалки приведена на рисунке:

В основе схемы - мультивибратор на транзисторах кт315а, он, периодически, подает импульсы на светодиоды VD1-VD4. Период следования и длительность импульсов определяются ёмкостями конденсаторов C5, C6 и сопротивлениями резисторов R6 и R7 (которые можно изменять). Схема работает не так как предполагалось но, на мой взгляд, получился неплохой эффект:

Подбором ёмкостей конденсаторов C1-С6 можно добиться разных эффектов мигания.

четверг, 29 декабря 2011 г.

Расчёт, в маткаде, регулировочной характеристики трёхфазного мостового преобразователя.

На рисунке 1 приведен мостовой тиристорный преобразователь который может осуществлять выпрямление трёхфазного напряжения либо инвертирование (если Lн - генератор), в зависимости от угла управления тиристорами и напряжения на нагрузке. Если бы в схеме на рисунке 1, вместо тиристоров, стояли бы диоды то такая схема осуществляла бы выпрямление, трёхфазного напряжения, и на нагрузке было бы некоторое среднее значение напряжения Ud0. Диоды в такой схеме открывались бы тогда когда ток в них стремился бы протекать в прямом направлении, в схеме с тиристорами момент открытия происходит тогда когда ток стремиться протекать в прямом направлении и на управляющий электрод подается импульс. Момент времени когда диод открывается (в аналогичной схеме с диодами) называют точкой естественной коммутации, её принимают за начало отсчёта а отрезок времени до следующей такой же точки представляют как 360^o (или 2π), угол коммутации принимают как часть от начала до момента подачи импульса управления на тиристор, в градусах или радианах.

Изменением угла управления изменяют среднее напряжение на нагрузке.

Регулировочная характеристика, управляемого, преобразователя - это зависимость среднего значения напряжения на нагрузке от угла управления.

Рисунок 1 - Трёхфазный мостовой тиристорный преобразователь ведомый сетью

Пусть индуктивность нагрузки Lн настолько велика что можно считать Lн→∞. Для расчёта регулировочной характеристики понадобится функция:

См. статью преобразование градусов в радианы и обратно, в маткаде. После определения функции нахождения косинуса в градусах пишется функция:

В качестве параметра Ud0 ей передается среднее напряжение нагрузки в схеме с диодами. Вертикальные линии вдоль которых пишется программа выбираются из окна Programming (есть не во всех версиях):

От туда же выбирается цикл for и знак присвоения ←. Вертикальную линию можно удлинить вставлением в неё ещё одной линии. Переменной (i) определяющей количество итераций (сколько раз выполняется то что в теле цикла) присваивается диапазон значений, который выбирается из окна Matrix:

От туда же выбирается верхний индекс:

Этот индекс определяет столбец матрицы. Подставив в функцию Ud напряжение на выходе для неуправляемого выпрямителя (Ud0) можно найти регулировочную характеристику трёхфазного мостового управляемого преобразователя с активно-индуктивной нагрузкой при Lн→∞. Для примера подставим 100В:

В правом столбце значения углов, в градусах, в левом - средние напряжения в вольтах.

По этой таблице можно построить график:

При углах до 90^o преобразователь находится в режиме выпрямления, после - в режиме инвертирования.

Если нагрузка такого преобразователя чисто активная то он не сможет перейти в режим инвертирования.

Рисунок 2 - Трёхфазный мостовой тиристорный преобразователь ведомый сетью с активной нагрузкой

Для расчёта регулировочной характеристики преобразователя с чисто активной нагрузкой напишем функцию:

Подставим 100В:

Построим график:

При угле управления больше 120^o напряжение на нагрузке Rн будет равно нулю.

среда, 21 декабря 2011 г.

Преобразование градусов в радианы и обратно, в маткаде.

Из единичной окружности:

Рисунок 1 - Единичная окружность

видно что каждому значению угла в радианах соответствует значение в градусах, например π это 180^o. Если взять какой либо угол и его значение в градусах поделить на его значение в радианах то получиться некоторое число (коэффициент), если взять какой либо другой угол и его значение в градусах поделить на его значение в радианах то получиться тоже самое число. Зная это число и значение любого угла в радианах можно найти значение этого угла в градусах умножив это число на значение в радианах. Аналогично, чтобы найти число для преобразования в радианы нужно, для любого угла, значение в радианах поделить на значение в градусах. Если представить значение π как часть окружности на которую (часть) можно поделить любое значение угла, в радианах, и что этой части соответствует значение 180^o, для значений в градусах, то можно записать выражение:

Где α - значение угла в радианах, β - значение, этого же, угла в градусах. Из этого выражения можно выразить α или β. В программе MathCAD можно написать функции для преобразований и пользоваться ими в расчётах:

Можно проверить функции подставив в них значения углов:

Тригонометрические функции в маткаде, по умолчанию, принимают значения в радианах:

Поэтому подстановка значений в градусах не даст требуемых результатов:

Если функция преобразования градусов в радианы, в окне программы, написаны выше то можно написать тригонометрические функции принимающие градусы и пользоваться ими вместе с обычными:

Можно написать отдельную функцию:

Если требуется уменьшить время вычисления то в функции можно сразу использовать коэффициент для преобразования:

Это может быть полезно когда используются циклы в которых присутствуют такие функции.

Калькулятор, справа вверху, может переводить радианы в градусы, для этого в верхнем поле вписывается: "гр" и в скобках значение угла в радианах, например:

гр(180)

После чего нажимается "=". Он даёт приблизительные ответы из за погрешности вычислений.

Также есть возможность перевода градусов в радианы, для этого аналогично используется функция "рд", например:

рд(пи)

Ответ также выводится с небольшой погрешностью.

Если вы используете браузер Internet Explorier то, для работы калькулятора, необходимо разрешить заблокированное содержимое.

суббота, 17 декабря 2011 г.

Преобразование ИНУН в ИТУН.

На рисунке 1 показан источник напряжения управляемый напряжением (ИНУН), он обозначен как β·Uy, где β-коэффициент передачи напряжения, Uy - управляющее напряжение. R -эквивалентное сопротивление источника.

Рисунок 1 - Ветвь с источником напряжения управляемым напряжением и ветвь с управляющим напряжением

Такую схему можно преобразовать к виду:

Рисунок 2 - Ветвь с источником тока управляемым напряжением Uy и ветвь с напряжением Uy

В этой схеме (рисунок 2) g·Uу - источник тока управляемый напряжением (ИТУН). g - передаточная проводимость, Uy - напряжение на элементе, в управляющей ветви, G - эквивалентная проводимость источника. Передаточную проводимость, в схеме на рисунке 2, можно найти по формуле:

Где β-коэффициент передачи напряжения, R - эквивалентное сопротивление источника (см. рисунок 1). Эквивалентную проводимость можно найти по формуле:

Схема на рисунке 2 эквивалентна схеме на рисунке 1.

суббота, 10 декабря 2011 г.

Изменение цвета свечения двухцветного светодиода, мультивибратором.

Мультивибратор, на транзисторах КТ315А, рассмотренный ранее выдает импульсы напряжения, почти прямоугольной формы, с коллекторов транзисторов, причём если в какой то момент времени на коллекторе одного из транзисторов будет импульс то на коллекторе другого будет пауза и наоборот. Длительность импульсов и длительность пауз можно менять, причём длительность импульса на коллекторе одного из транзисторов будет равной длительности паузы на коллекторе другого транзистора. Эти свойства мультивибратора можно использовать для изменения цвета свечения светодиода с общим катодом, с плавным переходом от одного цвета к другому:

Рисунок 1 - Схема с регулировкой цвета свечения светодиода.

VD1 - двухцветный светодиод. VD1 это, на самом деле, два светодиода с общим катодом, один из них излучает красный цвет, другой - зелёный. Выглядеть он может так:

Этот светодиод был вынут из телевизора, маркировки на нем не видно, но тип светодиода можно определить экспериментально. Из схемы на рисунке 1 видно что мультивибратор подает импульсы поочерёдно то на один анод светодиода то на другой, т.е. светодиод мигает зелёным и красным цветами, но если частота импульсов достаточно велика то человеческий глаз не сможет "уловить" это мигание и воспримет это как цвет полученный из смеси красного и зелёного. Если длительность горения зелёного намного больше длительности горения красного то будет виден зелёный, если длительность горения красного намного больше длительности горения зелёного то будет виден красный, если длительности примерно равны то будет виден жёлтый. Резистор R5 (см. рисунок 1) служит для ограничения тока светодиода (резисторов R1 и и R4 может быть не достаточно).

Если снизить частоту следования импульсов генерируемых мультивибратором (например увеличив ёмкости конденсаторов) то можно будет наблюдать поочерёдное горение красного и зелёного цветов. Примерную частоту можно определить пользуясь программой приведенной ранее, в статье про мультивибратор.

воскресенье, 4 декабря 2011 г.

Передаточная функция емкостного делителя.

На рисунке 1 представлен емкостной делитель напряжения:

Рисунок 1 - Емкостной делитель

найдем его передаточную функцию. Для этого определим напряжение на выходе:

напряжение на входе:

Поделив напряжение на выходе на напряжение на входе получим передаточную функцию емкостного делителя:

Из выражения 3 видно что эта функция представляет собой некоторое число зависящее от емкостей конденсаторов C1 и C2.

среда, 30 ноября 2011 г.

Особенно полезные Ccылки на сaйты по электротехнике и электронике

myrobot.ru - сайт о: роботах, робототехнике и микроконтроллерах. В разделе "шаг за шагом" доступным языком объясняется всё необходимое для построения робота на микроконтроллере.

cxem.net - сайт с множеством полезного для радиолюбителя (схемы, справочники, информация для новичков, программы и т.д.).

radiokot.ru - большое количество разнообразных схем и конструкций, раздел для начинающих, галерея Кота, форум с разными интересными темами и не менее интересными людьми

mkgt.ru/files/materials/358/book.pdf - элeктроника, микроэлектроника и автоматика, учeбник (долго загружаeтся, но содержит много полeзного).

www.oldradioclub.ru - caйт co cxeмами нa лaмпaх.

www.newlibrary.ru/genre/tehnika/radiotehnika - книги по радиотехнике.

radiosvalka.narod.ru - схемы, справочник, программы.

тут должен быть ещё один какой то сайт но его пока нет

microsin.ru - нa этом сайте есть статьи по применению микроконтроллepoв и исходники пpoгpaмм.

www.rcdesign.ru - cайт o pадиoупpавляемых мoдeлях.
www.labview.ru/forum/viewforum.php?f=4 - форум по мультисиму.

понедельник, 28 ноября 2011 г.

Преобразование ИНУТ в ИТУТ.

На рисунке 1 показан источник напряжения управляемый током (ИНУТ), он обозначен как: r·Iy , где: r-передаточное сопротивление, Iy - ток в управляющей ветви. R - эквивалентное сопротивление источника.

Рисунок 1 - Ветвь с источником напряжения управляемым током и ветвь с этим током

Такую схему можно преобразовать к виду:

Рисунок 2 - Ветвь с источником тока управляемым током Iy и ветвь с током Iy

В этой схеме (рисунок 2) α·Iу - источник тока управляемый током (ИТУТ). α - коэффициент передачи тока, Iy - ток в управляющей ветви, G - эквивалентная проводимость источника.
Коэффициент передачи тока, в схеме на рисунке 2, можно найти по формуле:

Где r-передаточное сопротивление, R - эквивалентное сопротивление источника (см. рисунок 1). Эквивалентную проводимость можно найти по формуле:

Схема на рисунке 2 эквивалентна схеме на рисунке 1.

среда, 23 ноября 2011 г.

интересные cсылки на интересные cайты

Разные лестницы Иакова.
myrobot.ru - сайт о: роботах, робототехнике и микроконтроллерах. В разделе "шаг за шагом" доступным языком объясняется всё необходимое для построения робота на микроконтроллере.

mkgt.ru/files/materials/358/book.pdf - элeктpoника, микроэлектроника и aвтоматика, учeбник (дoлгo загружается, нo содержит мнoгo пoлeзнoгo).

www.oldradioclub.ru - сайт со схемами на лампах.

www.newlibrary.ru/genre/tehnika/radiotehnika - книги по радиотехнике.

radiosvalka.narod.ru - cxeмы, справочник, программы.

microsin.ru - на этом сайте есть статьи по применению микроконтроллеров и исходники программ.

www.rcdesign.ru - сайт о радиоуправляемых моделях.

www.labview.ru/forum/viewforum.php?f=4 - форум по мультисиму.

суббота, 19 ноября 2011 г.

Усиление в схеме с общим эмиттером.

Ранее, в этом блоге был описан расчёт элементов схемы усилителя постоянного тока на транзисторе КТ315Б. Основным элементом осуществляющим усиление, в такой схеме, является транзистор. Проще всего понять процесс усиления можно сравнивая делитель напряжения, на резисторах, с той частью схемы где происходит усиление:

Рисунок 1 - а) усилитель, б) делитель напряжения

На рисунке 1б показан делитель напряжения, верхний резистор Rд1 имеет фиксированное
сопротивление которое не меняется, нижний резистор Rд2 является переменным (или подстроечным) резистором и его сопротивление зависит то положения движка. Представим этот резистор в виде блока, в который втекает ток Iупр и что положение движка меняется в зависимости от тока Iупр таким образом: чем больше ток Iупр тем ниже находится движок и следовательно сопротивление резистора Rд2 меньше, чем меньше ток Iупр тем выше находится движок и следовательно сопротивление резистора Rд2 больше. С некоторыми допущениями, схема на рисунке 1б аналогична схеме на рисунке 1а.
У биполярного транзистора, показанного на рисунке 1а, есть три вывода: эмиттер, коллектор и база по ним текут токи Iэ, Iк и Iб соответственно. Направления этих токов показаны на рисунке 1а стрелочками. Значения этих токов связаны друг с другом соотношением:

т.е. ток эмиттера Iэ складывается из тока базы Iб и тока коллектора Iк, но учитывая что ток базы Iб намного меньше тока коллектора Iк, пренебрегаем током базы Iб. Запишем выражение:

Т.е. полагаем что через транзистор от коллектора к эмиттеру течет ток коллектора Iк а ток базы просто втекает в транзистор (на самом деле это не так но это: помогает понять процесс усиления и упрощает расчёты). Приняв такое допущение можно записать:

Где h21э - коэффициент передачи тока транзистора в схеме с общим эмиттером, его приводят в справочниках по транзисторам. Этот коэффициент показывает во сколько раз ток коллектора больше тока базы, h21э - коэффициент усиления тока. Из схемы на рисунке 1а можно, по второму закону Кирхгофа, записать выражение для нахождения напряжения на выходе усилителя Uвых:

Подставив (3) в (4) получим:

Из выражения (5) можно найти напряжение на выходе усилителя зная ток базы.

h21э min =
h21э max =

суббота, 12 ноября 2011 г.

Расчёт схемы с ИТУТом методом узловых потенциалов пример.

В схеме с ИТУНом рассмотренной в предыдущей статье заменим ИТУН (источник тока управляемый напряжением) ИТУТом (источником тока управляемым током):

Рисунок 1 - Схема

a3 - коэффициент передачи тока ИТУТа, I3 - ток ветви с резистором G3 (обозначен на схеме).
Зададим исходные значения: G1=2, G2=2, G3=8, J1=4, a3=2.
G1-G3-проводимости соответствующих резисторов, J1 - ток источника J1.
Составим уравнения для узлов 1 и 2 методом узловых потенциалов:

Учитывая что потенциал узла 0 равен нулю найдем ток I3 по формуле:

Подставим это произведение (G3 на потенциал второго узла) уравнения 1:

В правой части уравнений 3 оставим только независимые источники тока (т.е. оставим J1) а всё остальное перенесём в левую:

Вынесем в обоих уравнениях потенциал второго узла за скобки:

Преобразуем систему уравнений 4 к матричному виду:

Полученная система уравнений узловых потенциалов в матричном виде не сильно отличается от той которая была составлена в предыдущей статье.
Подставим в систему уравнений 6 исходные данные:

Произведём расчёт потенциалов 1 и 2 методом Крамера для этого найдём определитель (детерминант) матрицы узловых потенциалов:

Далее заменим левый столбец матрицы узловых потенциалов столбцом матрицы столбца узловых токов и найдем определитель полученной таким образом матрицы:

Теперь заменим правый столбец матрицы узловых потенциалов столбцом матрицы столбца узловых токов и найдем определитель полученной матрицы:

Найдем потенциал первого узла:

Найдем потенциал второго узла:

Потенциал нулевого узла равен нулю. Теперь зная потенциалы всех узлов можно найти ток любой ветви и напряжение на любом элементе.

Ток находится как произведение проводимости элемента на напряжение на нем.

Напряжение на элементе находится как разность потенциалов между которыми находится этот элемент.

Ниже приведена программа расчёта потенциалов 1 и 2 схемы на рисунке 1 при задаваемых других исходных значениях:

суббота, 31 декабря 2011 г.

четверг, 29 декабря 2011 г.

среда, 21 декабря 2011 г.

суббота, 17 декабря 2011 г.

суббота, 10 декабря 2011 г.

воскресенье, 4 декабря 2011 г.

среда, 30 ноября 2011 г.

понедельник, 28 ноября 2011 г.

среда, 23 ноября 2011 г.

суббота, 19 ноября 2011 г.

суббота, 12 ноября 2011 г.