Рассмотрим схему на рисунке 1:
Это уравнение можно привести к более удобному виду для нахождения его корней. Поделим числитель и знаменатель дроби на 1/pC:
Умножим обе части уравнения на знаменатель дроби:
Раскроем скобки в первом слагаемом:
Выполним последнее преобразование для приведения уравнения к виду удобному для нахождения его корней:
Это квадратное уравнение и его корни можно найти через дискриминант. Характеристическое уравнение можно составить также определив сопротивление цепи относительно какой либо другой ветви, для примера найдем характеристическое уравнение относительно ветви с индуктивностью, для удобства изменим схему на рисунке 2:
Выполним последнее преобразование для приведения уравнения к виду удобному для нахождения его корней:
Это уравнение совпадает с уравнением полученным ранее (для схемы на рисунке 2) что подтверждает правильность решения.
Рисунок 1 - Схема
Получить характеристическое уравнение схемы можно определив выражение для её комплексного сопротивления приравняв его (выражение) к нулю и заменив в нем (в выражении) на p.
на p.
 на p.
на p.Найдем комплексное сопротивление схемы относительно ветви с источником E заменив  на p в сопротивлениях конденсатора и катушки. Источник E заменим перемычкой так как его сопротивление равно нулю. Схема на рисунке 1 преобразована для более удобного определения характеристического уравнения:
на p в сопротивлениях конденсатора и катушки. Источник E заменим перемычкой так как его сопротивление равно нулю. Схема на рисунке 1 преобразована для более удобного определения характеристического уравнения:
 на p в сопротивлениях конденсатора и катушки. Источник E заменим перемычкой так как его сопротивление равно нулю. Схема на рисунке 1 преобразована для более удобного определения характеристического уравнения:
на p в сопротивлениях конденсатора и катушки. Источник E заменим перемычкой так как его сопротивление равно нулю. Схема на рисунке 1 преобразована для более удобного определения характеристического уравнения:Рисунок 2 - Схема 2
Заменим последовательное соединение элементов R2 и pL (с одноименными сопротивлениями) одним элементом Zlr2(p):
Рисунок 3 - Схема 3
Сопротивление Zlr2(p) находиться по формуле:
Заменим параллельное соединение Zlr2(p) и 1/pC одним элементом:
Рисунок 4 - Схема 4
Zlсr2(p) находиться по формуле:
Заменим последовательное соединение оставшихся двух элементов одним элементом:
Рисунок 5 - Схема 5
Zэ(p) - сопротивление цепи относительно точек A и B (рисунок 1) которое находиться по формуле:
Приравняв это выражение к нулю получим характеристическое уравнение:Это уравнение можно привести к более удобному виду для нахождения его корней. Поделим числитель и знаменатель дроби на 1/pC:
Умножим обе части уравнения на знаменатель дроби:
Раскроем скобки в первом слагаемом:
Выполним последнее преобразование для приведения уравнения к виду удобному для нахождения его корней:
Это квадратное уравнение и его корни можно найти через дискриминант. Характеристическое уравнение можно составить также определив сопротивление цепи относительно какой либо другой ветви, для примера найдем характеристическое уравнение относительно ветви с индуктивностью, для удобства изменим схему на рисунке 2:
Рисунок 6 - Схема 6
Аналогично приведенному выше примеру найдем характеристическое уравнение определив сопротивление относительно точек C и D и приравняв это сопротивление нулю:
Это выражение также является характеристическим уравнением. Приведем это уравнение к виду удобному для нахождения его корней для начала для этого умножим числитель и знаменатель дроби на pC:
Умножим обе части уравнения на знаменатель дроби:
Раскроем скобки:Выполним последнее преобразование для приведения уравнения к виду удобному для нахождения его корней:
Это уравнение совпадает с уравнением полученным ранее (для схемы на рисунке 2) что подтверждает правильность решения.












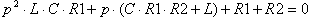


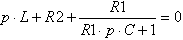



Комментариев нет:
Отправить комментарий