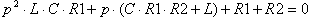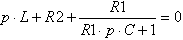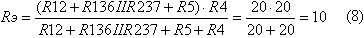Расчёт с преобразованием звезда-треугольник

В статье "расчет сопротивления схемы с преобразованием треугольник-звезда" рассчитывалось сопротивление схемы на рисунке 1 относительно точек А и В.

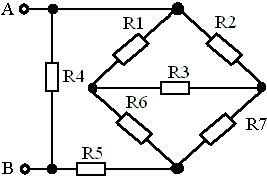
Рисунок 1 - Схема

Для упрощения расчёта было применено преобразование треугольника R1, R2, R3 в звезду. Для упрощения расчёта данной схемы можно также применить преобразование звезды образованной элементами R1, R3, R6 в треугольник. Преобразуем звезду R1, R3, R6 в треугольник R16, R31, R36:

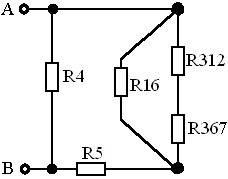
Рисунок 2 - Схема с преобразованной звездой R1, R3, R6 в треугольник R16, R31, R36.

Исходные данные будут такими же как и в статье где выполнялось преобразование треугольник-звезда:  R1=20, R2=20, R3=10, R4=20, R5=8, R6=4, R7=4.

Сопротивления резисторов R16, R31, R36 находятся по формулам:

Для нахождения сопротивления стороны треугольника нужно найти сумму сопротивлений прилегающих к данной стороне лучей звезды и произведения этих сопротивлений деленного на сопротивление оставшегося луча.

В схеме на рисунке 2 можно заменить параллельное соединение элементов R31 и R2 одним элементом R312 а параллельное соединение элементов R36 и R7 одним элементом R367:

Рисунок 3 - Схема с замененными параллельными соединениями элементов

 Сопротивления резисторов R312 и R367 рассчитываются по формулам:

Заменим последовательное соединение элементов R312 и R367 одним элементом R312367:

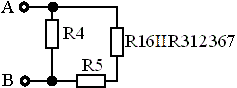
Рисунок 4 - Схема с преобразованным последовательным соединением R312 и R367

Сопротивление R312367 определяется по формуле:

Преобразуем параллельное соединение элементов R312367 и R16 одним элементом R16IIR312367:

Рисунок 5 - Схема с резистором R16IIR312367

Сопротивление R16IIR312367 находиться по формуле:

Схему на рисунке 5 можно преобразовать к одному элементу сопротивление которого будет равно сопротивлению схемы на рисунке 1 относительно точек А и В, для этого выражение для преобразования последовательного соединения элементов R5 и R16IIR312367 подставим в выражение для параллельного соединения R4 с последовательным соединением  R5 и R16IIR312367. 

Рисунок 6 - Эквивалентное сопротивление схемы 1

Rэ находиться по формуле:

Эквивалентное сопротивление схемы на рисунке 1 в результате расчёта получилось равным 10 такой же результат получился при расчёте приведенном в статье "расчет сопротивления схемы с преобразованием треугольник-звезда" что подтверждает правильность расчёта. Преобразование звезда-треугольник также упростило расчёт схемы.

Звезда-треугольник.

R1= Ом кОм МОм
R2= Ом кОм МОм
R3= Ом кОм МОм

R12= Ом кОм МОм
R13= Ом кОм МОм
R23= Ом кОм МОм
G12=См
G13=См
G23=См

Составление и расчёт характеристического уравнения схемы.

Рассмотрим схему на рисунке 1:

Рисунок 1 - Схема

Получить характеристическое уравнение схемы можно определив выражение для её комплексного сопротивления приравняв его (выражение) к нулю и заменив в нем (в выражении)на p.

Найдем комплексное сопротивление схемы относительно ветви с источником E заменив на p в сопротивлениях конденсатора и катушки. Источник E заменим перемычкой так как его сопротивление равно нулю. Схема на рисунке 1 преобразована для более удобного определения характеристического уравнения:

Рисунок 2 - Схема 2

Заменим последовательное соединение элементов R2 и pL (с одноименными сопротивлениями) одним элементом Zlr2(p):

Рисунок 3 - Схема 3

Сопротивление Zlr2(p) находиться по формуле:

Заменим параллельное соединение Zlr2(p) и 1/pC одним элементом:

Рисунок 4 - Схема 4

Zlсr2(p) находиться по формуле:

Заменим последовательное соединение оставшихся двух элементов одним элементом:

Рисунок 5 - Схема 5

Zэ(p) - сопротивление цепи относительно точек A и B (рисунок 1) которое находиться по формуле:

Приравняв это выражение к нулю получим характеристическое уравнение:

Это уравнение можно привести к более удобному виду для нахождения его корней. Поделим числитель и знаменатель дроби на 1/pC:

Умножим обе части уравнения на знаменатель дроби:

Раскроем скобки в первом слагаемом:

Выполним последнее преобразование для приведения уравнения к виду удобному для нахождения его корней:

Это квадратное уравнение и его корни можно найти через дискриминант. Характеристическое уравнение можно составить также определив сопротивление цепи относительно какой либо другой ветви, для примера найдем характеристическое уравнение относительно ветви с индуктивностью, для удобства изменим схему на рисунке 2:

Рисунок 6 - Схема 6

Аналогично приведенному выше примеру найдем характеристическое уравнение определив сопротивление относительно точек C и D и приравняв это сопротивление нулю:

Это выражение также является характеристическим уравнением. Приведем это уравнение к виду удобному для нахождения его корней для начала для этого умножим числитель и знаменатель дроби на pC: 

Умножим обе части уравнения на знаменатель дроби:

Раскроем скобки:

Выполним последнее преобразование для приведения уравнения к виду удобному для нахождения его корней:

Это уравнение совпадает с уравнением полученным ранее (для схемы на рисунке 2) что подтверждает правильность решения.

Расчет сопротивления схемы с преобразованием треугольник-звезда.

Рассмотрим схему приведенную на рисунке 1:

Рисунок 1 - Исходная схема

Допустим необходимо найти сопротивление схемы относительно точек A и B. Заданы сопротивления резисторов: R1=20, R2=20, R3=10, R4=20, R5=8, R6=4, R7=4. Преобразуем треугольник сопротивлений R1, R2, R3 в звезду сопротивлений R12, R23, R13:

Рисунок 2 - Схема с преобразованным в звезду треугольником 

Сопротивления R12, R13, R23 найдены по формулам 1-3: 

 Чтобы найти сопротивление луча звезды надо произведение сопротивлений прилегающих к нему сторон треугольника разделить на сумму сопротивлений всех сторон треугольника. 

 Преобразуем последовательное соединение резисторов R13 и R6 в резистор R136 и аналогично   преобразуем последовательное соединение резисторов R23 и R7 в резистор R237:

Рисунок 3 - Схема3

Сопротивления резисторов R136 и R237 найдены по формулам 4 и 5:

Преобразуем параллельное соединение резисторов R136 и R237 в резистор R136IIR237:

Рисунок 4 - Схема4

Найдем R136IIR237 по формуле 6:

Далее преобразуем схему 4 к виду:

Рисунок 5 - Схема5

Найдем сопротивление которое стоит справа:

Теперь, заменой параллельного соединения резисторов, в схеме на рисунке 5, одним резистором Rэ, находится эквивалентное сопротивление всей схемы:

Найдем Rэ:

Преобразование треугольника R1, R2, R3 в звезду R12, R23, R13 упростило расчёт эквивалентного сопротивления схемы относительно точек А и B в данном примере.

Треугольник-звезда.

R1= Ом кОм МОм
R2= Ом кОм МОм
R3= Ом кОм МОм

R12= Ом кОм МОм
R13= Ом кОм МОм
R23= Ом кОм МОм

Пример расчёта переходной характеристики по передаточной функции.

Пусть задана передаточная функция динамического звена:

Переходная характеристика находиться по формуле:

Для нахождения переходной характеристики, для данного случая, можно разложить передаточную функцию W(p) на сумму простых дробей по формуле:

Для разложения найдены: корни уравнения и  

коэффициенты K1, K2, K3:

Подстановкой найденных p1, p2, K1, K2, K3 в уравнение (3) найдено разложение на сумму простых дробей передаточной функции (1):

Для нахождения обратного преобразования Лапласа функции (4) можно воспользоваться выражением (5):

Где b и a - некоторые константы.

Применением выражения (5) к функции (4) найдена переходная характеристика:

Построить график можно в программе Scilab которую можно бесплатно скачать с официального сайта http://www.scilab.org/. Текст для построения графика характеристики (6), скопированный из окна программы Scilab, приведен ниже:

-->t=0:0.1:10;

-->plot(t,((-2/3)*%e^(-t))+((1/6)*%e^(-4*t))+(1/2));

-->xtitle("Переходная характеристика","t","h(t)");

-->xgrid;

На рисунке 1 приведён получившийся график:

Рисунок 1 - График h(t)