Метод двух узлов является частным случаем метода узловых потенциалов. Данным методом могут быть рассчитаны цепи содержащие два неустранимых узла. Для расчёта методом двух узлов находят напряжение между зтими узлами Uab по формуле:
Где Ek - напряжение источника ЭДС k-ой ветви, Gk - проводимость k-ой ветви, Jk - ток источника тока k-ой ветви.
Затем находят токи в ветвях без источников тока по формуле:
Где Ek - напряжение источника ЭДС k-ой ветви, Gk - проводимость k-ой ветви, Jk - ток источника тока k-ой ветви.
Затем находят токи в ветвях без источников тока по формуле:
Ток в ветви с источником тока равен току этого источника.
Рассмотрим расчёт методом двух узлов на примере расчёта схемы на рисунке 1:
Рисунок 1 - Схема для расчёта методом двух узлов
Пусть в этой схеме E1=10 В, R1=0.1 Ом, R2=4 Ом, R3=8 Ом, E3=-20 В, J4=40 А. Найдём проводимости резисторов:
Далее рассчитаем напряжение между узлами а и b по формуле (1):
Затем найдём токи в ветвях по формуле (2):
Рассчтаем мощность выделяющуюся в резисторах Pр и мощность отдаваемую источниками Pи для проверки балланса мощностей:
Мощность выделяющаяся в резисторах, с допустимой погрешностью, равна мощности выделяемой источниками следовательно балланс мощностей выполнен и расчёт произведён верно.
Пример 2
При расчёте схемы методом двух узлов можно применить немного другой подход.
Рассмотрим схему:
Рисунок 2 - Схема 2 для расчёта методом двух узлов
Направления токов в ветвях, кроме тех в которых стоят источники тока, выбраны произвольно. В схеме имеется 2 узла: узел a и узел b. Будем считать что потенциал узла b равен нулю, напряжение Uab, в таком случае, равно потенциалу узла a. Определим проводимости каждой ветви, при этом учтём то что:
сопротивление источника ЭДС (с одинарной стрелочкой в кружке) равно нулю а его проводимость равна бесконечности,
сопротивление источника тока (с двумя стрелочками в кружке) равно бесконечности а его проводимость равна нулю.
Проводимость ветви с током I1 будет равна G1=1/R1, проводимости источников ЭДС равны нулю поэтому они не учитываются (их можно считать перемычками на которых есть напряжение).
Проводимость ветви с током I2 будет равна G2=1/R2 источник опять же не учитывается.
проводимость ветви с током I3 равна нулю (т.к. проводимость источника тока равна нулю (источник тока можно считать разрывом через который течёт ток) ).
Проводимость ветви с током I4 равна нулю т.к. проводимость источника тока равна нулю, можно считать что в этой ветви разрыв и резистор R3 ничего не меняет.
Пусть в этой схеме E1=4 В, R1=10 Ом, R2=5 Ом, R3=2 Ом, E2=6 В, E3=10 В, J1=5 А, J2=4 А. Найдём проводимости резисторов:
Найдём напряжение Uab по формуле (1)
E1 записан со знаком минус т.к. его эдс (стрелочка внутри) направлена от узла а
E2 записано со знаком + т.к. его эдс направлена к узлу а
E3 записано со знаком + т.к. его эдс направлено к узлу а
J1 записан со знаком - т.к. его ток направлен от узла а
J2 записан со знаком + т.к. его ток направлен к узлу а
в знаменателе записана сумма проводимости первой ветви и второй, оставшиеся две ветви имеют проводимость равную нулю поэтому не записываются.
(В первом случае направления источников эдс учитывались а алгебраических знаках перед значениями этих эдс).
Ток I3=J1=5 т.к. источник тока создаёт в ветви ток равный току этого источника,
Ток I4=J2=4 т.к. источник тока создаёт в ветви ток равный току этого источника.
Найти ток I1 можно по закону Ома и второму закону Кирхгофа:
Аналогично можно найти ток I2:
Для составления баланса мощностей необходимо найти напряжение на источнике тока J2 (см. рисунок 2), найдём напряжение UJ2 на источнике тока J2:
Составим баланс мощностей:
Pи- отдаваемая и принимаемая мощность источников, Pп-мощность принимаемая резисторами. Если направление тока совпадает с направлением эдс источника эдс то это эдс записывается со знаком "+" если нет то со знаком "-". Если напряжение на источнике тока направлено противоположно току этого источника то ток этого источника записывается в уравнение баланса мощностей со знаком "+" если направление напряжения и тока совпадают то со знаком "-".








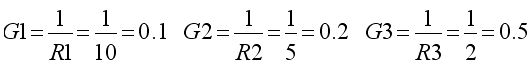





Токи в цепях пожалуйста расставьте для наглядности. Не очень понятно как мы расчитывали ток в 1 и 3 ветвях.
ОтветитьУдалитьДа эта статья написана немного "криво" когда у автора появится свободное время будут внесены исправления.
Удалитьсамое время, полтора года прошло
Удалитьвсе понятно спасибо
ОтветитьУдалить