Ёмкостные фильтры могут применятся для сглаживания выпрямленного напряжения. Простейший ёмкостный фильтр представляет собой конденсатор большой ёмкости соединённый паралельно с нагрузкой. В статье второй закон коммутации упоминалось о невозможности скачка напряжения на конденсаторе и его плавном изменении при изменениях в цепи, это свойство конденсатора положено в основу работы сглаживающего ёмкостного фильтра. Если конденсатор поставить на выходе однофазного однополупериодного выпрямителя синусоидального переменного тока и подсоединить пареалельно ему (конденсатору) нагрузку то напряжение на нагрузке будет сглаженным но пульсации напряжения всёже будут присудствовать. Рассмотрим схему:
Здесь e(t) - источник напряжения имитирующий выходное напряжение однополупериодного однофазного выпрямителя, Re - внутреннее сопротивление этого источника, С - конденсатор, Rn - активная нагрузка (например резистор). Определить форму напряжения на нагрузке при переходном процессе или в установившемся режиме можно составив и исследовав математическую модель фильтра. Для описания процессов происходящих в фильтре можно составить уравнение состояния данной цепи. Уравнение состояния для данной цепи представляет собой зависимость производной напряжения конденсатора по времени от напряжения конденсатора и времени. Для упрощения составления математической модели цепи представляющей собой уравнение состояния необходимо выбрать направления токов в ветвях, пронумеровать узлы и выбрать направления обходов контуров на рисунке ниже выбран один контур который пригодиться при расчётах.
Составим уравнение по первому закону Кирхгофа для узла 1:
Выразим ток Ic:
Преобразуем выражение согласно второму закону коммутации и закону Ома:
Выразим от сюда производную напряжения конденсатора по времени:
В этом выражении неизвестным является только ток Ie для того чтобы его найти составим уравнение по второму закону кирхгофа для контура показанного на рисунке 2 преобразуем выражение используя закон Ома и выразим ток Ie:
Подставим найденное выражение для тока Ie в уравнение (4) и получим уравнение состояния:
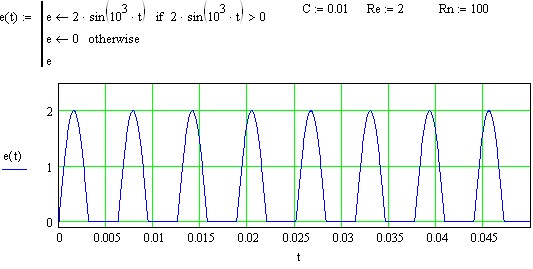
Решением уравнения (10) при заданных начальных условиях (начальном t и начальном Uc) является функция описывающая изменение напряжения конденсатора во времени. Таким образом чтобы выяснить форму кривой напряжения на нагрузке (оно же и напряжение на конденсаторе) необходимо задать начальное время, начальное напряжение на конденсаторе и решить уравнение (10). Это уравнение может быть решено численнными методами например методом Эйлера, методом Рунге-Кутта. Далее будет приведён пример расчёта уравнения (10) в программе MathCAD. На примере ниже заданны значения элементов схемы и задана функция имитирующая изменение напряжения выпрямленного однофазным однополупериодным выпрямителем. Циклическая частота выпрямтенного и выпрямляемого напряжений 1000 Гц, амплитуда выпрямленного напряжения 2 В, ёмкость конденсатора 0.01 Ф (довольно таки большая ёмкость), внутреннее сопротивление источника 2 Ом, сопротивление нагрузки 100 Ом, на графике ниже показано изменение напряжения источника e(t) от времени.
Далее записываем составленное уравнение состояния (10) в виде функции, затем записываем начальное значение напряжения на конденсаторе в переменную (в примере X0). Пусть в начальный момент времени конденсатор разряжен и отсчёт времени начинается с нуля тогда напряжение на конденсаторе в момент времени t=0 равно нулю оно и записывается в переменную X0. Далее какой либо переменной (в примере Y) присваивается значение возвращаемое функцией Rkadapt в качестве первого параметра этой функции записывается начальное значение напряжения, в качестве втрого параметра передаётся начальное значение времени, в качестве третьего конечное значение времени (0.05 с) до которого ведётся расчёт, четвёртый параметр количество рассчитываемых точек которое следует выбрать так чтобы расчёт был с заданной точностью и при этом не следует выбирать слишком большое количество точек так как расчёт может затянуться, в качестве последнего параметра передаётся идентификатор функции записанной ранее как уравнение состояния цепи. Присвоив переменным (в примере uc и time)расчитанные значения напряжения и времени так как показано в примере ниже можно построить на одном графике зависимости e(t) и напряжения на конденсаторе (uc) от времени (time) записав в левой части графика uc поставив запятую и записав e(t), в нижней части графика записывается time,t.
Напряжение на нагрузке показано красной кривой, из графика видно как оно изменяется и можно оценить пульсации напряжения на нагрузке. Пульсации напряжения на нагрузке сильно зависят от ёмкости конденсатора и внутреннего сопротивления источника и слабо от сопротивления нагрузки если оно на много больше чем внутреннее сопротивление источника. Соединение Re и С как на рисунке 1 представляет собой Г-образный RC фильтр поэтому при установлении в источник питания конденсатора в качестве фильтра необходимо учитывать внутреннее сопротивление источника выпрямленного напряжения представляющего собой используемый выпрямитель поставленный на выходе источника выпрямляемого напряжения. Внутреннее сопротивление такого источника может быть определено эксперементально или расчитано. Изменяя значения C и Re можно проследить как изменяются пульсации напряжения на нагрузке (оно же и на конденсаторе). Ниже приведены примеры напряжения нагрузки при разных значениях ёмкости C и сопротивления Re.
При С=0.03, Re=2:
При С=0.002, Re=2:
Рисунок 1 - Схема фильтра с источником
Рисунок 2 - Схема фильтра с источником и обозначениями для расчёта
Выразим ток Ic:
Преобразуем выражение согласно второму закону коммутации и закону Ома:
Выразим от сюда производную напряжения конденсатора по времени:
В этом выражении неизвестным является только ток Ie для того чтобы его найти составим уравнение по второму закону кирхгофа для контура показанного на рисунке 2 преобразуем выражение используя закон Ома и выразим ток Ie:
Подставим найденное выражение для тока Ie в уравнение (4) и получим уравнение состояния:
Решением уравнения (10) при заданных начальных условиях (начальном t и начальном Uc) является функция описывающая изменение напряжения конденсатора во времени. Таким образом чтобы выяснить форму кривой напряжения на нагрузке (оно же и напряжение на конденсаторе) необходимо задать начальное время, начальное напряжение на конденсаторе и решить уравнение (10). Это уравнение может быть решено численнными методами например методом Эйлера, методом Рунге-Кутта. Далее будет приведён пример расчёта уравнения (10) в программе MathCAD. На примере ниже заданны значения элементов схемы и задана функция имитирующая изменение напряжения выпрямленного однофазным однополупериодным выпрямителем. Циклическая частота выпрямтенного и выпрямляемого напряжений 1000 Гц, амплитуда выпрямленного напряжения 2 В, ёмкость конденсатора 0.01 Ф (довольно таки большая ёмкость), внутреннее сопротивление источника 2 Ом, сопротивление нагрузки 100 Ом, на графике ниже показано изменение напряжения источника e(t) от времени.
Далее записываем составленное уравнение состояния (10) в виде функции, затем записываем начальное значение напряжения на конденсаторе в переменную (в примере X0). Пусть в начальный момент времени конденсатор разряжен и отсчёт времени начинается с нуля тогда напряжение на конденсаторе в момент времени t=0 равно нулю оно и записывается в переменную X0. Далее какой либо переменной (в примере Y) присваивается значение возвращаемое функцией Rkadapt в качестве первого параметра этой функции записывается начальное значение напряжения, в качестве втрого параметра передаётся начальное значение времени, в качестве третьего конечное значение времени (0.05 с) до которого ведётся расчёт, четвёртый параметр количество рассчитываемых точек которое следует выбрать так чтобы расчёт был с заданной точностью и при этом не следует выбирать слишком большое количество точек так как расчёт может затянуться, в качестве последнего параметра передаётся идентификатор функции записанной ранее как уравнение состояния цепи. Присвоив переменным (в примере uc и time)расчитанные значения напряжения и времени так как показано в примере ниже можно построить на одном графике зависимости e(t) и напряжения на конденсаторе (uc) от времени (time) записав в левой части графика uc поставив запятую и записав e(t), в нижней части графика записывается time,t.
Напряжение на нагрузке показано красной кривой, из графика видно как оно изменяется и можно оценить пульсации напряжения на нагрузке. Пульсации напряжения на нагрузке сильно зависят от ёмкости конденсатора и внутреннего сопротивления источника и слабо от сопротивления нагрузки если оно на много больше чем внутреннее сопротивление источника. Соединение Re и С как на рисунке 1 представляет собой Г-образный RC фильтр поэтому при установлении в источник питания конденсатора в качестве фильтра необходимо учитывать внутреннее сопротивление источника выпрямленного напряжения представляющего собой используемый выпрямитель поставленный на выходе источника выпрямляемого напряжения. Внутреннее сопротивление такого источника может быть определено эксперементально или расчитано. Изменяя значения C и Re можно проследить как изменяются пульсации напряжения на нагрузке (оно же и на конденсаторе). Ниже приведены примеры напряжения нагрузки при разных значениях ёмкости C и сопротивления Re.
При С=0.03, Re=2:
При C=0.01 Re=5:
При C=0.03 Re=5:
При С=0.002, Re=2:
При C=0.01, Re=0.2:
При C=0.002, Re=0.3:
Из графиков видно что лучшее сглаживание напряжения происходит при большей ёмкости конденсатора и при большем внутреннем сопртивлении источника при этом длительность переходного процесса увеличивается и напряжения на нагрузке устанавливается дольше (в примерах с увеличенными С и Re установившееся значение выходит из рассчитываемого диапазона). Улучшить сглаживание напряжения можно поставив на выходе выпрямителя резистор для добавления сопротивления Re но это снизит КПД устройства, можно увеличить ёмкость конденсатора но это увеличит размеры устройства поэтому для маломощных компактных устройств рекомендуется увеличение сопротивления а для мощных не критичных к размерам увеличение ёмкости.















Крутотень! Давно искал, спасибо огромное!
ОтветитьУдалитьАвтор, можете выложить маткадовский файл с этими расчетами?
Ссылка:
Удалитьhttp://yadi.sk/d/1FykuQvbAskTc