Если в схеме присутствует источник напряжения управляемый напряжением (ИНУН) то для этой схемы можно составить уравнения методом контурных токов и найти токи во всех ветвях. Расчёт методом контурных токов рассмотрим на примере расчёта схемы:
Рисунок 1 - Схема
В схеме, на рисунке 1, есть два источника напряжения. E1-неуправляемый источник (его напряжение не изменяется). Другой источник - управляемый, он управляется напряжением U2, напряжение этого источника будет в β раз больше напряжения U2.
Пусть для схемы на рисунке 1 заданы сопротивления резисторов, напряжение источника E1 и коэффициент передачи напряжения β:
R1=1 Ом,
R2=1 Ом,
R3=100 Ом,
R4=10 Ом,
R5=10 Ом,
R6=20 Ом,
E1=40 В,
β =80.
Для схемы, на рисунке 1, выберем:
1) направления токов во всех ветвях,
2) независимые контуры и
3) направления обходов этих контуров.
Число независимых контуров определяется из уравнения:
Контуры = (число ветвей - число ветвей с источником тока) - (число узлов - 1)
Направления обходов контуров могут выбираться в любую сторону. Направления токов ветвей тоже могут выбираться в любую сторону.
В первом уравнении (для контура I11) контурный ток I11 умножается на сумму сопротивлений принадлежащих контуру I11 (это произведение берется со знаком плюс). Контуру I11 принадлежат сопротивления: R1, R2, R3. Далее, в первом уравнении, со знаком минус, записывается произведение контурного тока I22 и сопротивления R2 (т.к. R2 - общее сопротивление для контуров I11 и I22). После чего, в первом уравнении, со знаком минус, записывается произведение тока I33 и сопротивления R3 (т.к. R3 - общее сопротивление для контуров I11 и I33). Если у того контура для которого записывается уравнение и контура для которого записывается отрицательное слагаемое нет общего сопротивления то в уравнение это слагаемое не записывается или записывается произведение нуля на контурный ток контура для которого записывается слагаемое. В правой части первого уравнения записывается напряжение источника β⋅U2 со знаком плюс т.к. направление обхода контура I11 не совпадает с направлением напряжения источника β⋅U2 (оно указано справа от этого источника, от плюса к минусу). Второе уравнение (для контура I22) записывается аналогично. Произведение тока I11 и сопротивления R2 (общее для контуров I11 и I22) записывается со знаком минус, во втором уравнении. Произведение тока I22 и суммы сопротивлений входящих в контур I22 записывается со знаком плюс. Произведение тока I22 и сопротивления R5 (общего для контуров I22 и I33) записывается со знаком минус. В правой части уравнения записывается напряжение источника E1 со знаком минус т.к. направление обхода контура I22 совпадает с направлением напряжения источника E1 (оно указано сверху от этого источника, от плюса к минусу). Третье уравнение (для контура I33) записывается аналогично. Произведение тока I11 и сопротивления R3 (общее для контуров I11 и I33) записывается со знаком минус, в третьем уравнении. Произведение тока I22 и сопротивления R5 (общее для контуров I22 и I33) записывается со знаком минус. Произведение тока I33 и суммы сопротивлений: R3, R5, R6 (общих для контура I33) записывается со знаком плюс. В правой части уравнения записывается напряжение источника β⋅U2 со знаком минус (т.к. направление обхода контура I33 совпадает с направлением напряжения источника β⋅U2).
Далее (для расчёта контурных токов) представим напряжение U2 как произведение сопротивления R2 и тока I2:
Ток I11 берется со знаком плюс т.к. обход контура I11 направлен в туже сторону что и ток I2, ток I22 берется со знаком минус т.к. обход контура I22 направлен в туже сторону что и ток I2.
Подставим уравнение (3) в уравнение (2):
Вынесем за скобки токи I11 и I33 в первом и втором уравнениях:
Представим систему уравнений (8) в матричном виде:
Дадим матрице с сопротивлениями обозначение Z, а матрице с источником -E1 обозначение E и подставим в них исходные значения:
Найдем определитель (детерминант) матрицы Z:
Найти определитель матрицы 3го порядка можно таким способом:
1) справо от матрицы записываются два первых столбца (получается матрица с пятью столбцами),
2) элементы расположенные на главной диагонали (первая диагональ с лева на право с верху в низ, включает элементы: Δ11, Δ22, Δ33) перемножаются,
3) элементы (Δ12, Δ23, Δ31) расположенные на диагонали находящейся с права от главной диагонали перемножаются,
4) перемножаются элементы (Δ13, Δ21, Δ32) расположенные на крайней правой диагонали,
5) эти три полученных произведения суммируются,
6) элементы расположенные на побочной диагонали (первая диагональ с права на лево с верху в низ, включает элементы: Δ13, Δ22, Δ31) перемножаются,
7) элементы (Δ11, Δ23, Δ32) расположенные на диагонали находящейся с права от побочной диагонали перемножаются,
8) перемножаются элементы (Δ12, Δ21, Δ33) расположенные на диагонали расположенной с право от той которая расположена с право от побочной,
9) эти три полученных произведения суммируются,
10) из первой полученной суммы вычитается вторая.
Заменим первый столбец матрицы Z матрицей-столбцом E и найдем определитель полученной матрицы:
Заменим второй столбец матрицы Z матрицей-столбцом E и найдем определитель полученной матрицы:
Заменим третий столбец матрицы Z матрицей-столбцом E и найдем определитель полученной матрицы:
Поделив первый определитель ΔI11 на определитель матрицы Z найдем контурный ток I11:
Поделив второй определитель ΔI22 на определитель матрицы Z найдем контурный ток I22:
Пусть для схемы на рисунке 1 заданы сопротивления резисторов, напряжение источника E1 и коэффициент передачи напряжения β:
R1=1 Ом,
R2=1 Ом,
R3=100 Ом,
R4=10 Ом,
R5=10 Ом,
R6=20 Ом,
E1=40 В,
β =80.
Для схемы, на рисунке 1, выберем:
1) направления токов во всех ветвях,
2) независимые контуры и
3) направления обходов этих контуров.
Число независимых контуров определяется из уравнения:
Контуры = (число ветвей - число ветвей с источником тока) - (число узлов - 1)
Направления обходов контуров могут выбираться в любую сторону. Направления токов ветвей тоже могут выбираться в любую сторону.
Рисунок 2 - Схема с выбранными направлениями токов ветвей и выбранными контурами
Рассмотрим систему уравнении записанную методом контурных токов:
В первом уравнении (для контура I11) контурный ток I11 умножается на сумму сопротивлений принадлежащих контуру I11 (это произведение берется со знаком плюс). Контуру I11 принадлежат сопротивления: R1, R2, R3. Далее, в первом уравнении, со знаком минус, записывается произведение контурного тока I22 и сопротивления R2 (т.к. R2 - общее сопротивление для контуров I11 и I22). После чего, в первом уравнении, со знаком минус, записывается произведение тока I33 и сопротивления R3 (т.к. R3 - общее сопротивление для контуров I11 и I33). Если у того контура для которого записывается уравнение и контура для которого записывается отрицательное слагаемое нет общего сопротивления то в уравнение это слагаемое не записывается или записывается произведение нуля на контурный ток контура для которого записывается слагаемое. В правой части первого уравнения записывается напряжение источника β⋅U2 со знаком плюс т.к. направление обхода контура I11 не совпадает с направлением напряжения источника β⋅U2 (оно указано справа от этого источника, от плюса к минусу). Второе уравнение (для контура I22) записывается аналогично. Произведение тока I11 и сопротивления R2 (общее для контуров I11 и I22) записывается со знаком минус, во втором уравнении. Произведение тока I22 и суммы сопротивлений входящих в контур I22 записывается со знаком плюс. Произведение тока I22 и сопротивления R5 (общего для контуров I22 и I33) записывается со знаком минус. В правой части уравнения записывается напряжение источника E1 со знаком минус т.к. направление обхода контура I22 совпадает с направлением напряжения источника E1 (оно указано сверху от этого источника, от плюса к минусу). Третье уравнение (для контура I33) записывается аналогично. Произведение тока I11 и сопротивления R3 (общее для контуров I11 и I33) записывается со знаком минус, в третьем уравнении. Произведение тока I22 и сопротивления R5 (общее для контуров I22 и I33) записывается со знаком минус. Произведение тока I33 и суммы сопротивлений: R3, R5, R6 (общих для контура I33) записывается со знаком плюс. В правой части уравнения записывается напряжение источника β⋅U2 со знаком минус (т.к. направление обхода контура I33 совпадает с направлением напряжения источника β⋅U2).
Далее (для расчёта контурных токов) представим напряжение U2 как произведение сопротивления R2 и тока I2:
Выразим ток I2 через контурные токи I11 и I22:
Подставим уравнение (3) в уравнение (2):
Подставим уравнение (4) в систему уравнений (1)
В первом и третьем уравнениях перенесем напряжение источника в левую часть:
Раскроем скобки в первом и третьем уравнениях:
Вынесем за скобки токи I11 и I33 в первом и втором уравнениях:
Представим систему уравнений (8) в матричном виде:
Дадим матрице с сопротивлениями обозначение Z, а матрице с источником -E1 обозначение E и подставим в них исходные значения:
Найдем определитель (детерминант) матрицы Z:
Найти определитель матрицы 3го порядка можно таким способом:
1) справо от матрицы записываются два первых столбца (получается матрица с пятью столбцами),
2) элементы расположенные на главной диагонали (первая диагональ с лева на право с верху в низ, включает элементы: Δ11, Δ22, Δ33) перемножаются,
3) элементы (Δ12, Δ23, Δ31) расположенные на диагонали находящейся с права от главной диагонали перемножаются,
4) перемножаются элементы (Δ13, Δ21, Δ32) расположенные на крайней правой диагонали,
5) эти три полученных произведения суммируются,
6) элементы расположенные на побочной диагонали (первая диагональ с права на лево с верху в низ, включает элементы: Δ13, Δ22, Δ31) перемножаются,
7) элементы (Δ11, Δ23, Δ32) расположенные на диагонали находящейся с права от побочной диагонали перемножаются,
8) перемножаются элементы (Δ12, Δ21, Δ33) расположенные на диагонали расположенной с право от той которая расположена с право от побочной,
9) эти три полученных произведения суммируются,
10) из первой полученной суммы вычитается вторая.
Заменим первый столбец матрицы Z матрицей-столбцом E и найдем определитель полученной матрицы:
Заменим третий столбец матрицы Z матрицей-столбцом E и найдем определитель полученной матрицы:
Поделив первый определитель ΔI11 на определитель матрицы Z найдем контурный ток I11:
Поделив второй определитель ΔI22 на определитель матрицы Z найдем контурный ток I22:
Поделив первый определитель ΔI11 на определитель матрицы Z найдем контурный ток I11:
Теперь выразим токи ветвей через контурные токи и рассчитаем токи ветвей.
Ток I1 равен контурному току I11 т.к. они направлены в одну сторону и ветви с током I1 не принадлежат другие контура:
Ток I2 уже был выведен ранее:
Аналогично выведем и определим другие токи:
Если ток получается отрицательным то значит он направлен в сторону противоположную выбранной:
Рисунок 3 - Схема с правильными направлениями токов.
Ниже приведена программа для расчёта токов ветвей схемы на рисунке 1 при введенных исходных значениях:









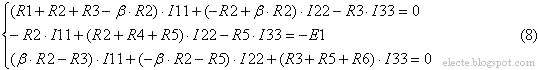


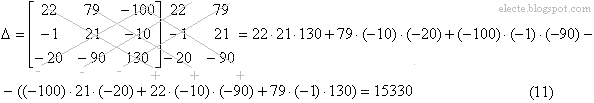













Спасибо большое!!! Мне очень помогла данная информация!
ОтветитьУдалитьСпасибо большое!!!!
ОтветитьУдалитьСпосибо огромное
ОтветитьУдалить