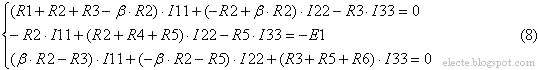Второй закон Кирхгофа.

  Второй закон (правило) Кирхгофа - алгебраическая сумма напряжений на элементах контура электрической цепи равна нулю.
Контур электрической цепи - замкнутый проводящий ток путь образованный элементами электрической цепи.
Рассмотрим схему на рисунке 1:

Рисунок 1 - Схема с одним контуром

В этой схеме присутствуют: источник ЭДС и резисторы R1, R2 и R3; эти элементы образуют замкнутый путь проводящий ток т.е. контур. Напряжение на источнике ЭДС равно E и направлено так как показано на рисунке 1 стрелочкой справа от источника. Стрелка на условном обозначении источника направлена в сторону противоположную направлению напряжения на источнике ЭДС (иногда это запутывает при расчёте схем но так принято обозначать источник ЭДС). Направления падений напряжений на резисторах указаны стрелками (рис. 1). Для составления уравнения, по второму закону Кирхгофа, необходимо выбрать направление обхода контура (по часовой стрелке или против). В схеме на рисунке 1 показано направление по часовой стрелке. Запишем уравнение по второму закону Кирхгофа:

Напряжения резисторов вошли в левую часть уравнения со знаком плюс т.к. направление обхода контура совпадает с направлениями напряжений на резисторах. Напряжение источника ЭДС E вошло в правую часть со знаком плюс т.к. направление обхода контура не совпадает с направлением напряжения источника. Можно также записать напряжение источника в левой части уравнения со знаком минус (что, в принципе, тоже самое):

Уравнение (2) больше подходит для определения второго закона Кирхгофа приведенного выше.

Напряжения совпадающие по направлению с обходом контура записаны со знаком плюс а напряжение источника не совпадающее с обходом контура - со знаком минус и вся эта алгебраическая сумма равна нулю. Теперь, из выражения (2), зная три каких либо напряжения можно найти четвёртое. Обычно расчёт цепи сводится к нахождению токов во всех ветвях или потенциалов всех узлов т.к. зная эти величины (токи ветвей или потенциалы узлов), сопротивления всех элементов и напряжения источников ЭДС (и токи всех источников тока) можно найти напряжение на любом элементе и ток любого элемента. В схеме на рисунке 1 для определения напряжений U1, U2 и U3 достаточно знать ток I т.к. он одинаков для всех элементов цепи (R1, R2, R3, E). Умножением тока I на сопротивление R1 находится напряжение U1, умножением тока I на сопротивление R2 находится напряжение U2, умножением тока I на сопротивление R3 находится напряжение U3. Учитывая это можно привести уравнение (1) к виду:

Из уравнения (3) можно найти ток I. Т.к. контур один то и ток в уравнении один но если схема содержит больше одно контура то и токов будет больше. Вынеся ток I за скобки и поделив обе части уравнения на сумму сопротивлений R1, R2 и R3 получаем уравнение для нахождения тока I, но этот ток можно найти и другим способом например заменой последовательного соединения резисторов R1, R2 и R3 одним резистором R123 и делением напряжения E на сопротивление резистора R123.

Сопротивление резистора R123 равно сумме сопротивлений резисторов R1, R2 и R3. Ток находится из уравнения:

     Если в контуре содержится больше одного источника ЭДС то уравнение, по второму закону (правилу) Кирхгофа, составляется аналогично.

Рисунок 2 - Схема с двумя источниками ЭДС

Запишем уравнение, по второму закону Кирхгофа, для контура в схеме на рисунке 2:

Напряжение E2 источника E2 записано в правой части уравнения со знаком минус т.к. оно совпадает по направлению с обходом контура. Заменяя напряжения на резисторах произведениями тока I на сопротивления резисторов получим уравнение:

Из уравнения (6) может быть найден ток I.

Если схема имеет больше одного контура то Закон (правило) Кирхгофа все равно выполняется для всех контуров. Уравнения по второму закону Кирхгофа, в таком случае, составляются аналогично тому как в примерах выше. Отличие будет только в том что необязательно для всех элементов будет один и тот же ток. В случае если схема имеет больше одного контура можно считать что через каждый элемент течет свой ток. Напряжение на элементе, в таком случае, находится умножением сопротивления этого элемента (если этот элемент например резистор) на ток данного элемента.

Рисунок 3 - Часть схемы имеющей больше одного контура

Рисунок 4 - Часть схемы имеющей больше одного контура и ветвь из двух элементов

Рисунок 4 - Часть схемы имеющей больше одного контура, ветвь из двух элементов и элементы напряжения на на которых имеют направления не совпадающие с выбранным направлением обхода контура

О том что такое узлы и ветви можно узнать из предыдущей статьи.

При составлении уравнений по второму закону Кирхгофа не стоит слишком много времени уделять выбору направлений обходов контуров и направлений токов (

они (направления обходов и токов) выбираются произвольно) так как реальные направления токов определяются при решении этих уравнений.

Пример:

Направление напряжения на элементе R1 такое же как и направление тока этого элемента по тому что принято считать что ток течёт от большего потенциала к меньшему а напряжение направлено также (от большего потенциала к меньшему).

Первый закон Кирхгофа.

1) Первый закон (правило) Кирхгофа - алгебраическая сумма токов сходящихся в узле равна нулю.

Ветви - это проводящие участки цепи между узлами.

Узел - это область соединения двух (или трёх) и более ветвей.

Алгебраическая сумма - это сумма в которую входят слагаемые со знаком плюс и со знаком минус.

На рисунке ниже показан узел в котором соединяются четыре ветви с токами: I1, I2, I3, I4.

Рисунок 1 - Узел с ветвями

Направления токов показаны стрелочками. От узла направлены токи I1 и I2, к узлу направлены токи I3 и I4. Примем направления к узлу - положительными, а от узла - отрицательными. Запишем, с учётом выбранных положительных и отрицательных направлений токов, уравнение по первому закону Кирхгофа для узла на рисунке 1:

Ток I1 вошел в уравнение (1) со знаком минус так как этот ток направлен от узла (см. рисунок 1).
Ток I2 входит в уравнение (1) со знаком минус по той же причине. Токи I3 и I4 входят в уравнение (1) со знаком плюс так как они направлены к узлу (см. рисунок 1). Вся эта алгебраическая сумма равна нулю.
     Токи I1 и I2 можно перенести в правую часть уравнения с противоположным знаком:

Также можно поступить и с любым уравнением записанным по первому закону Кирхгофа.

Учитывая это можно дать другое определение первого закона (правила) Кирхгофа:

2) сумма токов входящих в узел равна сумме токов выходящих из него.

Уравнение (2) можно привести к виду:

перенеся в правую часть уравнения токи I3 и I4 с противоположным знаком.
   Уравнение (3) можно привести к виду:

Тоже самое можно проделать с любым уравнением записанным по первому закону Кирхгофа. Это значит что не имеет значения то какое направление (от узла или к узлу) принято за положительное а какое за отрицательное, главное чтобы все одинаковые направления имели один знак а все противоположные другой. 

    Иногда бывает так что один узел принимается за два и более при невнимательном осмотре схемы что приводит к ошибкам в расчётах. Рассмотрим схему на рисунке 2:

 Рисунок 2 - Схема с одним узлом

В этой схеме один узел, для этого узла можно составить уравнение по первому закону Кирхгофа:

Токи в узлах не протекают т.к. узел имеет один потенциал на всем его протяжении и на всей его площади.   

Расчёт, методом контурных токов, схемы с ИНУНом.

Если в схеме присутствует источник напряжения управляемый напряжением (ИНУН) то для этой схемы можно составить уравнения методом контурных токов и найти токи во всех ветвях. Расчёт методом контурных токов рассмотрим на примере расчёта схемы:

Рисунок 1 - Схема

В схеме, на рисунке 1, есть два источника напряжения. E1-неуправляемый источник (его напряжение не изменяется). Другой источник - управляемый, он управляется напряжением U2, напряжение этого источника будет в β раз больше напряжения U2.
Пусть для схемы на рисунке 1 заданы сопротивления резисторов, напряжение источника E1 и коэффициент передачи напряжения β:
R1=1 Ом,
R2=1 Ом,
R3=100 Ом,
R4=10 Ом,
R5=10 Ом,
R6=20 Ом,
E1=40 В,
 β =80.
Для схемы, на рисунке 1, выберем:
1) направления токов во всех ветвях,
2) независимые контуры и
3) направления обходов этих контуров.
Число независимых контуров определяется из уравнения:
Контуры = (число ветвей - число ветвей с источником тока) - (число узлов - 1)
Направления обходов контуров могут выбираться в любую сторону. Направления токов ветвей тоже могут выбираться в любую сторону. 

 Рисунок 2 - Схема с выбранными направлениями токов ветвей и выбранными контурами 

Рассмотрим систему уравнении записанную методом контурных токов: 

В первом уравнении (для контура I11) контурный ток I11 умножается на сумму сопротивлений принадлежащих контуру I11 (это произведение берется со знаком плюс). Контуру I11 принадлежат сопротивления: R1, R2, R3. Далее, в первом уравнении, со знаком минус, записывается произведение контурного тока I22 и сопротивления R2 (т.к. R2 - общее сопротивление для контуров I11 и I22). После чего, в первом уравнении, со знаком минус, записывается произведение тока I33 и сопротивления R3 (т.к. R3 - общее сопротивление для контуров I11 и I33). Если у того контура для которого записывается уравнение и контура для которого записывается отрицательное слагаемое нет общего сопротивления то в уравнение это слагаемое не записывается или записывается произведение нуля на контурный ток контура для которого записывается слагаемое. В правой части первого уравнения записывается напряжение источника β⋅U2 со знаком плюс т.к. направление обхода контура I11 не совпадает с направлением напряжения источника β⋅U2 (оно указано справа от этого источника, от плюса к минусу). Второе уравнение (для контура I22) записывается аналогично. Произведение тока I11 и сопротивления R2 (общее для контуров I11 и I22) записывается со знаком минус, во втором уравнении. Произведение тока I22 и суммы сопротивлений входящих в контур I22 записывается со знаком плюс. Произведение тока I22 и сопротивления R5 (общего для контуров I22 и I33) записывается со знаком минус. В правой части уравнения записывается напряжение источника E1 со знаком минус т.к. направление обхода контура I22 совпадает с направлением напряжения источника E1 (оно указано сверху от этого источника, от плюса к минусу). Третье уравнение (для контура I33) записывается аналогично. Произведение тока I11 и сопротивления R3 (общее для контуров I11 и I33) записывается со знаком минус, в третьем уравнении.  Произведение тока I22 и сопротивления R5 (общее для контуров I22 и I33) записывается со знаком минус. Произведение тока I33 и суммы сопротивлений: R3, R5, R6 (общих для контура I33) записывается со знаком плюс. В правой части уравнения записывается напряжение источника β⋅U2 со знаком минус (т.к. направление обхода контура I33 совпадает с направлением напряжения источника β⋅U2).
 Далее (для расчёта контурных токов) представим напряжение U2 как произведение сопротивления R2 и тока I2:

Выразим ток I2 через контурные токи I11 и I22:

Ток I11 берется со знаком плюс т.к. обход контура I11 направлен в туже сторону что и ток I2, ток I22 берется со знаком минус т.к. обход контура I22 направлен в туже сторону что и ток I2.
Подставим уравнение (3) в уравнение (2):

Подставим уравнение (4) в систему уравнений (1)

В первом и третьем уравнениях перенесем напряжение источника в левую часть:

Раскроем скобки в первом и третьем уравнениях: 

Вынесем за скобки токи I11 и I33 в первом и втором уравнениях:

Представим систему уравнений (8) в матричном виде:

Дадим матрице с сопротивлениями обозначение Z, а матрице с источником -E1 обозначение E и подставим в них исходные значения:

Найдем определитель (детерминант) матрицы Z:

Найти определитель матрицы 3го порядка можно таким способом:
1) справо от матрицы записываются два первых столбца (получается матрица с пятью столбцами),
2) элементы расположенные на главной диагонали (первая диагональ с лева на право с верху в низ, включает элементы: Δ11, Δ22, Δ33) перемножаются,
3) элементы (Δ12, Δ23, Δ31) расположенные на диагонали находящейся с права от главной диагонали перемножаются,
4) перемножаются элементы (Δ13, Δ21, Δ32) расположенные на крайней правой диагонали,
5) эти три полученных произведения суммируются,
6) элементы расположенные на побочной диагонали (первая диагональ с права на лево с верху в низ, включает элементы: Δ13, Δ22, Δ31) перемножаются,
7) элементы (Δ11, Δ23, Δ32) расположенные на диагонали находящейся с права от побочной диагонали перемножаются,
8) перемножаются элементы (Δ12, Δ21, Δ33) расположенные на диагонали расположенной с право от той которая расположена с право от побочной,
9) эти три полученных произведения суммируются,
10) из первой полученной суммы вычитается вторая.

Заменим первый столбец матрицы Z матрицей-столбцом E и найдем определитель полученной матрицы:

Заменим второй столбец матрицы Z матрицей-столбцом E и найдем определитель полученной матрицы:

Заменим третий столбец матрицы Z матрицей-столбцом E и найдем определитель полученной матрицы:

Поделив первый определитель ΔI11 на определитель матрицы Z найдем контурный ток I11:

Поделив второй определитель ΔI22 на определитель матрицы Z найдем контурный ток I22:

Поделив первый определитель ΔI11 на определитель матрицы Z найдем контурный ток I11:

Теперь выразим токи ветвей через контурные токи и рассчитаем токи ветвей.

Ток I1 равен контурному току I11 т.к. они направлены в одну сторону и ветви с током I1 не принадлежат другие контура:

Ток I2 уже был выведен ранее:

Аналогично выведем и определим другие токи:

Если ток получается отрицательным то значит он направлен в сторону противоположную выбранной:

Рисунок 3 - Схема с правильными направлениями токов.

Ниже приведена программа для расчёта токов ветвей схемы на рисунке 1 при введенных исходных значениях:

R1=Ом
R2=Ом
R3=Ом
R4=Ом
R5=Ом
R6=Ом
β=
E1=В

I1=А
I2=А
I3=А
I4=А
I5=А
I6=А

Светодиодная мигалка на микроконтроллере ATmega8.

Использование микроконтроллеров существенно упрощает построение светодиодных мигалок. Светодиодная мигалка - это, наверное, одно из самых подходящих устройств для изготовления новичками в области построения схем на микроконтроллерах. Здесь приведен пример построения мигалки и исходный код для микроконтроллера ATmega8 на языке C++.
На сайте myrobot.ru в разделе "шаг за шагом" понятным языком описано как программировать микроконтроллеры и часть информации, приведенной здесь, взята от туда. Рассмотрим схему приведенную на рисунке:

Пусть кнопка SB1 будет для переключения режима мигания, а кнопка SB2 для изменения частоты мигания. Исходный код приведен ниже:


 int main(void)        
   {
DDRD = 0xff;            /* все выводы порта D сконфигурировать как выходы */
DDRC = 0x00;      //выводы порта С сконфигурировать как входы

PORTC = 0xff; // установить "1" на всех выводах порта C,
// включаем подтягивающие резисторы

int i=0; //для задержек
int j=0; //для смены битов порта D
int d=20; //для изменения периода миганий
int sw=0; //для изменения режимов миганий

while (1)          // Бесконечный цикл
{
if (!(PINC & (1<<PINC4))) //если логический ноль на 4 бите порта С
{
sw++; //преключить режим миганий
if(sw>4)sw=0;
}
if (!(PINC & (1<<PINC3))) //если логический ноль на 3 бите порта С
{
d+=20; //увеличить период миганий
if(d>260)d=20;
}

switch(sw)
{
case 0:
DDRD |= 1<<j;
for(i=0;i<d;i++)_delay_us(50);
DDRD &= ~(1<<j);
for(i=0;i<d;i++)_delay_us(50);
j++;
if(j>3)j=0;
break;
case 1:
DDRD |= 1<<j;
for(i=0;i<d;i++)_delay_us(50);
DDRD &= ~(1<<j);
for(i=0;i<d;i++)_delay_us(50);
j--;
if(j<0)j=3;
break;
case 2:
DDRD &= ~(1<<j);
for(i=0;i<d;i++)_delay_us(50);
DDRD |= 1<<j;
for(i=0;i<d;i++)_delay_us(50);
j++;
if(j>3)j=0;
break;
case 3:
DDRD &= ~(1<<j);
for(i=0;i<d;i++)_delay_us(50);
DDRD |= 1<<j;
for(i=0;i<d;i++)_delay_us(50);
j--;
if(j<0)j=3;
break;
case 4:
DDRD=0xff;
for(i=0;i<d;i++)_delay_us(50);
DDRD=0x00;
for(i=0;i<d;i++)_delay_us(50);
break;
}
}

   }

При каждой итерации цикла while проверяется нажатие кнопок. Если нажата кнопка SB1 то переменная sw инкрементируется. Если переменная sw равна нулю (это проверяет команда switch) то в нулевой бит порта D записывается единица, потом происходит задержка, после чего в этот бит записывается ноль, затем снова задержка, потом переменная j инкрементируется и, если кнопка SB1 не была нажата, то все повторяется для следующего бита и таким образом происходит "движение светодиода", когда переменная j становится больше трех, ей присваивается ноль и все повторяется. Если нажимается кнопка SB1 то sw увеличивается и если она была равна нулю то она становиться равной единице и тогда происходит тоже что и при sw равной нулю только j теперь не инкрементируется а декрементируется (за счёт этого "движение светодиода" происходит в другую сторону) а при становлении j меньше нуля ей присваивается 3 и всё повторяется. Если sw равно двум или трем то происходит тоже только "бегущий светодиод" инвертирован, потому что порядок записи нуля и единицы в биты портов изменен. Если sw равно четырем то мигают все светодиоды. Если нажата кнопка SB2 то переменная d увеличивается на 20 и т.о. увеличиваются все задержки, следовательно увеличивается период мигания светодиодов при всех режимах. Если d>260 то ей снова присваивается значение 20 и период миганий резко уменьшается (частота увеличивается).

Исходный код компилировался в hex файл программой WinAVR. hex файл записывался в микроконтроллер программой PonyProg.