В статье расчёт цепи в маткаде рассматривался рассчёт простой цепи с активными элементами в программе маткад. Практически применимые схемы, как правило, более сложные в таких случаях использование таких САПРов как маткад значительно упрощает рассчёт. Для расчёта сложных цепей в программе маткад можно использовать метод уравнений Кирхгофа который может быть применён к любой цепи в заданый момент времени. Для рассчёта сложных цепей в которых нет нелинейных элементов (или эти элементы аппроксимированы линейными) применимы и более простые методы например метод узловых потенциалов на примере которого рассмотрим рассчёт УЗЧ (усилителя звуковых частот) на ОУ (операционных усилителях) рисунок 1.
Рисунок 1 - УЗЧ на ОУ
На вход усилителя подаётся синусоидальное напряжение с заданной частотой, на выходе стоит заданная нагрузка. Усилитель состоит из трёх каскадов. Для расчёта усилителя в маткаде принципиальная схема заменяется эквивалентной схемей замещения. Операционный усилитель в простейшем случае может быть заменён четырёхполюсником на входе которого стоит резистор с сопротивлением равным входному сопротивлению каскада а на выходе стоит последовательное соединение источника напряжения с напряжениением равным произведению напряжения на входе каскада на коэффициент его усиления и резистора с сопротивлением равным выходному сопротивлению каскада. Опуская остальные подробности и переходя к расчёту схемы в маткаде приводиться схема замещения данного УЗЧ на рисунке 2.
Рисунок 2 - Схема замещения УЗЧ на ОУ
Для начала задаются исходные данные:
Мнимая единица задана на всякий случай, сопротивления заданы в омах, ёмкости в фарадах, частота в герцах, напряжение е1 в вольтах, коэффициенты усиления каскадов безразмерные.
Далее идёт расчёт напряжений на выходе ОУ.
Для рассчёта методом узловых потенциалов необходимо, для каждого узла, найти сумму проводимостей ветвей присоединённых к нему и присвоить переменным как это сделано ниже. Например для узла 2 (номера узлов в кружках на схеме) проводимость G22 будет состоять из суммы проводимостей резисторов R3, R4 и Rвых1 источник Eвых1 не считается. Проводимость конденсатора записывается как произведение мнимой единицы, циклической частоты, ёмкости этого конденсатора со знаком минус. Далее записываются проводимости ветвей между двумя узлами (между котоыми есть элемент с проводимостью) со знаком минус например проводимость ветви между узлами 1 и 2 записывается G12 или G21 равна проводимости резистора R3 со знаком минус. Для узлов к которым подсоединены ветви с источниками напряжения записываются переменные с номерами соответствующих узлов. В данном случае когда все источники одним концом подсоединены к нулевому узлу (земле) который не считается имеющимся переменным J1, J2, J5, J8 присваивается отношение напряжения источника к сопротивлению резистора в ветви с источником со знаком плюс если ток направлен к узлу и со знаком минус если наоборот. Для узла к которому подсоединён источник Е1 и не обозначенного на рисунке применён перенос источников ЭДС (на рисунке не показано, оставлена первоначальная схема).
Создаются две матрицы первая с чслом столбцов и строк равным числу узлов, вторая с числом строк равным числу узлов. В первую матрицу на главную диагональ записываются переменные G11-G88. В остальные ячейки записываются проводимости между узлами номера которых соответствуют номеру столбца и номеру строки матрицы как в примере ниже. Первая матрица должна получиься симметричной относительно главной диагонали если в неё подставить численные значения проводимостей. Во вторую матрицу в строки с номерами узлов к которым подсоединены источники напряжения соответственно записываются переменные J1, J2, J5, J8.
В не занятые ячейки матриц записываются нули.
Умножив обращённую матрицу G на матрицу J получим матрицу потенциалов узлов с первого по восьмой. Перемножать матрицы можно только в таком порядке как показано на примере иначе маткад выведет ошибку. Для обращения к элементам матрицы U можно использовать нижний индекс. Функцией Re находится действительная часть числа, функцией Im мнимая.
Теперь можно найти требуемые токи и их действующие значения. Действующее значение тока находится как корень квадратный из суммы квадратов действительной и мнимой составляющей значения тока.
В маткаде существует возможность расчёта по системе уравнений без использования матриц, такой расчёт (для метода контурных токов) рассмотрен в статье Расчёт систем уравнений в маткаде, метод контурных токов. В статье расчёт схемы методом узловых потенциалов пример 2 рассмотрен более подробно более простой пример расчёта схемы методом узловых потенциалов.
В не занятые ячейки матриц записываются нули.
Умножив обращённую матрицу G на матрицу J получим матрицу потенциалов узлов с первого по восьмой. Перемножать матрицы можно только в таком порядке как показано на примере иначе маткад выведет ошибку. Для обращения к элементам матрицы U можно использовать нижний индекс. Функцией Re находится действительная часть числа, функцией Im мнимая.
Теперь можно найти требуемые токи и их действующие значения. Действующее значение тока находится как корень квадратный из суммы квадратов действительной и мнимой составляющей значения тока.



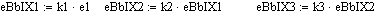




Комментариев нет:
Отправить комментарий