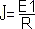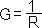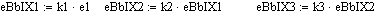Расчёт систем уравнений в маткаде, метод контурных токов.

Расчёт системы уравнений  в программе  mathcad  рассмотрим для уравнений составленных для схемы:

Рисунок 1 - Схема для расчёта.

В статье расчёт в маткаде цепи методом узловых потенциалов рассматривался пример расчёта схемы методом узловых потенциалов при этом уравнения для расчёта были составлены в виде матриц. В программе mathcad есть возможность расчитывать обычные системы уравнений. Рассмотрим метод контурных токов. Для составления уравнений методом контурных токов в схеме необходимо: выбрать направления токов ветвей (в ветви с источником тока по направлению источника тока в остальных ветвях произвольно), выбрать направления обходов независимых контуров, пронумеровать узлы один из которых будет опорным. Число контуров (и число уравнений) можно найти по формуле:

Где в-число всех ветвей, вит-число ветвей с источниками тока, у-число узлов Ч-число контуров равное числу уравнений.

Рисунок 2 - Схема с выбранными обходами контуров, ветвей и пронумерованными узлами.

Третий контурный ток показан для наглядности, уравнение для него не составляется так как в нём есть источник тока, этот контурный ток равен току источника тока J. В программе  mathcad присваиваем переменным заданные значения:

Затем пишем Given и уравнения для первого и второго контуров:

Знак равно выбирается с панели программирования!  В ставых версиях маткада может не быть программирования. Чтобы составить уравнение для первого контура записывается произведение первого контурного тока на сумму сопротивлений входящих в этот контур (записывается со знаком плюс), со знаком минус записываются произведения других контурных токов на сопротивления общие с контуром первым и другими, после знака равно записываются напряжения источников напряжения и произведения токов источников токов на сопротивления общие для первого контура и контуров включающих эти источники тока со знаком плюс если направление обхода контура не совпадает с направлением источника напряжения (для напряжения источника напряжения) или обходом контура включающего источник тока (для произведения токов источников токов на сопротивления общие для первого контура и контуров включающих эти источники тока ) и со знаком минус если напрявления совпадают. Аналогично составляется второе уравнение. Направление источника напряжения показано на рисунке 2 не внутри источника а снаружи от плюса к минусу. После записи уравнений пишется Find и в скобках, через запятую, неизвестные и ставится значёк стрелочки как на примере ниже:

Переменным контурных токов I11 и I22 присваиваются найденные значения. После расчитываются токи как в примере ниже:

Если ветвь входит в один контурный ток то ток этой ветви равен этому контурному току. Если ветвь входит в несколько контуров то ток этой ветви равен алгебраической сумме контурных токов в которые входит эта ветвь, в эту сумму со знаком плюс записываются контурные токи с направлениями совпадающими с направлением ветви и со знаком минус записываются контурные токи направления которых не совпадают с направлением ветви. Если значение тока получилось со знаком минус то ток в схеме на самом деле в ветви с этим током течёт в направлении противоположном вбранному. Для проверки расчёта можно использовать программу Micro-Cap.

 Временной анализ показывает правильность расчёта для ветвей с сопротивлениями R1, R2, R4, R5. Для расчёта схемы в маткаде методом контурных токов можно использовать системы уравнений заданные в виде матриц как это делелось в примере с расчётом методом узловых потенциалов. Метод контурных токов целесообразно использовать для схем с числом уравнений по второму закону Кирхгофа меньшим чем по первому. Для расчёта каких либо других уравнений или систем уравнений также можно использовать Given и Find при этом знак равенства в уравнениях ставится жирный с панели программирования иначе  mathcad будет выдавать ошибку.



Текст расчёта цепи в маткаде.

Ниже приведён полный текст расчёта расмотренного в статье расчёт цепи в маткаде.

Схема для которой произведён данный расчёт можно найти в статье расчёт цепи в маткаде.

Перемножение массивов чисел в маткаде.

При выполнении расчётов может возникнуть необходимость в перемножении большого количества чисел что при расчёте вручную может занять много времени. Использованием программы MathCAD можно упростить данную процедуру. Если например в виде таблицы задана зависимость тока от напряжения для какого либо прибора и необходимо найти зависимость  сопротивления этого прибора от тока то сделать это можно используя, рассмотренные ниже, способы.

1. Первый способ.

Токи и напряжения задаются в виде транспонированных матриц-строк. Транспонирование матрицы - это замена её сторок её столбцами или наоборот. При транспонировании матрицы-строки она становится матрицей-столбцом. В примере транспонирование матриц с заданными значениями сделано для экономии места. Далее единица делится на матрицу I и это умножается на транспонированную матрицу U (обязательно умножается в таком порядке как в примере). Потом какой либо переменной присваивается диапазон значений от 0 до числа элементов матриы I или U (число их элементов должно быть равно). Для вывода результата используется переменная в нижнем индексе которой, через запятую, прописаны идентификаторы переменной которой присваивался диапазон. После этой переменной ставится знак равно и (если установлен автоматический расчёт) автоматически выводится таблица отношений заданных напряжений к заданным токам в том пордке в котором они прописаны в матрицах U и I.

 В примере R - это матрица - произведение матрицы - столбца 1/I на матрицу строку U. На главной диагонали матрицы R располагаются произведения соответствующих элементов матриц 1/I и U например 1/I₀*U₀=R_0,0=100  или 1/I₁*U₁=R_1,1=57.143 (нумерация элементов матриц в маткаде начинается с нуля).

2. Второй способ.

Этот способ годится для версий маткада имеющих встроенный язык программирования. В маткаде есть функция last() она возвращает номер последнего элемента матрицы иденитфикатор которой вписан в скобки стоящие после идентификатора этой функции. Для программирования пишется какая либо переменная после неё ставится знак присвоения потом на панели программирования выбирается Add Line (добавить линию)(в данном случае выбирается 3 раза). Потом какой либо переменнной (например i) присваивается начальное значение 0 (в программе присвоение обозначается стрелочкой). На панели программирования выбирается цикл while и условие цикла прописывается как в примере (выполнение пока i меньше или равно (не больше) номера последнего элемента заданной матрицы) в теле цикла создаётся ещё одна линия и в ней прописыавется присвоение i-ому элементу матрицы r значения отнощения i-го элемента матрицы U к i-му элементу матрицы I. В следующей строке тела цикла прописывается команда увеличения переменной i на единицу (инкремент i). Под циклом записывается r, таким образом массив r из программы запишется в R2.

 Псле рассчётов можно построить зависимости в виде графиков. Второй способ целесообразно исползовать когда требуется автоматизировать остальной расчёт, первый способ для простого получения значений без остального расчёта прописанного в маткаде или без связи с ним. Во втором примере в цикле можно прописать и более сложное выражение. Язык программирования в маткаде достаточно прост и лёгок в освоении использоване этого языка может ускорить решение определённых задач на которые у неопытного программиста может уйти много времени при использовании других языков. Возможность построения графиков в маткаде избавляет от необходимости использования GDI или других средств вывода графики. Но средствами маткада не заменить возможности GDI поэтому при решении более сложных задач придётся перейти на более сложный язык.

Замена источников.

Рассмотрим замену источника напряжения источником тока преобразовав схему:

Рисунок 1 - Схема для преобразования

Последовательное соединение источника E1 и резистора R можно заменить параллельным соединением источника тока J и резистора R. Ток этого источника тока расчитывается по форуле:

Где E1 - напряжение источника напряжения E1, R - сопротивление резистора R.

Проводимость резистора соединённого параллельно с источником тока находится по формуле:

После преобразования схема будет выглядеть следующим образом:

Рисунок 2 - Преобразованая схема

Возможно и обратное преобразование когда параллельное соединение источника тока J (с значением тока равным J) и резистора заменяется последовательным соединением источника напряжения и резистора. В этом случае напряжение источника напряжения находится по формуле:

Или, если задана проводимость резистора G, по формуле:

Где J - ток источника тока. 

ЭДС и внутреннее сопротивление реального источника питания можно найти экспериментально воспользовавшись формулами (6) и (7) приведенными в статье "нахождение внутреннего сопротивления и ЭДС источника".



Введение фиктивной прводимости.

Метод введения фиктивной проводимости (или сопротивления) может применяться для преобразования схемы к виду пригодному для расчёта методом узловых потенцалов. При  переносе источника ЭДС как в рассмотренном ранее примере происходит устранение ветви с источником ЭДС без электрического сопротивления при этом также устраняется один узел это приводит к уменьшению уравнений необходимых для расчёта схемы методом узловых потенциалов что упрощает расчёт. Метод введения фиктивной проводимости не уменьшает числа узлов но имеет свои достоинства например более простую реализацию кода на языке программирования при написании программы расчёта схемы на ЭВМ. Рассмотрим схему из предыдущего примера:

Рисунок 1 - Схема для преобразования

Суть метода заключается в том что в ветвь с источником ЭДС (E1) вводятся два последовательно соединённых резистора с равными по величине и противоположными по знаку сопротивлениями.

После введения сопротивлений схема будет выглядеть так:

Рисунок 2 - Схема с введёнными фиктивными сопротивлениями

R может быть каким угодно например 1 Ом. Схему на рисунке 2 можно расчитывать методом узловых потенциалов. Сопротивления можно заменить проводимостями. Последовательное соединение источника напряжения и резистора с положительным сопротивлением можно заменить параллельным соединением источника тока и резистора с положительной проводимостью, такое преобразование рассмотрено в следующем примере.



Перенос источников ЭДС.

  Иногда для выполнения расчёта схемы или её упрощения необходимо выполнить преобразование этой схемы. Например для расчёта схемы методом узловых потенциалов необходимо исключить ветви содержащие только источники напряжения. На рисунке 1 показана схема которую можно преобразовать к виду пригодному для расчёта методом узловых потенциалов.

Рисунок 1 - Схема для преобразования

На схеме видна ветвь в которой содержится один источник напряжения Е1. Данную схему можно заменить схемой на рисунке 2.

Рисунок 2 - Схема эквивалентная схеме на рисунке 1

Напряжения источников E1^|, E1^||, E1^||| равны напряжению источника E1 поэтому соединение источников таким образом не меняет потенциал узла к которому они подсоединены. Можно заметить ветвь в которой находятся два источника напряжения (Е1 и Е1^|) их напряжения равны по величине и противоположны по направлению. Напряжения источников Е1 и  Е1^| компенсируют друг друга и не вносят в работу схемы никаких изменений поэтому их можно исключить из схемы.

Рисунок 3 - Схема с исключёнными источниками  Е1 и  Е1^|

Схему на рисунке 3 можно использовать для расчёта методом узловых потенциалов. Можно заметит что ветвь с током i1 не влияет на работу остальной части схемы. Схему на рисунке 3 можно заменить схемой:

Рисунок 4 - Преобразованная схема

Схема на рисунке 4 эквивалентна пердыдущим.

Расчёт в маткаде цепи методом узловых потенциалов.

   В статье расчёт цепи в маткаде рассматривался рассчёт простой цепи с активными элементами в программе маткад. Практически применимые схемы, как правило, более сложные в таких случаях использование таких САПРов как маткад значительно упрощает рассчёт. Для расчёта сложных цепей в программе маткад можно использовать метод уравнений Кирхгофа который может быть применён к любой цепи в заданый момент времени. Для рассчёта сложных цепей в которых нет нелинейных элементов (или эти элементы аппроксимированы линейными) применимы и более простые методы например метод узловых потенциалов на примере которого рассмотрим рассчёт УЗЧ (усилителя звуковых частот) на ОУ (операционных усилителях) рисунок 1.

Рисунок 1 - УЗЧ на ОУ

На вход усилителя подаётся синусоидальное напряжение с заданной частотой, на выходе стоит заданная нагрузка. Усилитель состоит из трёх каскадов. Для расчёта усилителя в маткаде принципиальная схема заменяется эквивалентной схемей замещения. Операционный усилитель в простейшем случае может быть заменён четырёхполюсником на входе которого стоит резистор с сопротивлением равным входному сопротивлению каскада а на выходе стоит последовательное соединение источника напряжения с напряжениением равным произведению напряжения на входе каскада на коэффициент его усиления и резистора с сопротивлением равным выходному сопротивлению каскада. Опуская остальные подробности и переходя к расчёту схемы в маткаде приводиться схема замещения данного УЗЧ на рисунке 2.

Рисунок 2 - Схема замещения УЗЧ на ОУ

Для начала задаются исходные данные:

Мнимая единица задана на всякий случай, сопротивления заданы в омах, ёмкости в фарадах, частота в герцах, напряжение е1 в вольтах, коэффициенты усиления каскадов безразмерные.

 Далее идёт расчёт напряжений на выходе ОУ.

Для рассчёта методом узловых потенциалов необходимо, для каждого узла, найти сумму проводимостей ветвей присоединённых к нему и присвоить переменным как это сделано ниже. Например для узла 2 (номера узлов в кружках на схеме) проводимость G22 будет состоять из суммы проводимостей резисторов R3, R4 и Rвых1 источник Eвых1 не считается. Проводимость конденсатора записывается как произведение мнимой единицы, циклической частоты, ёмкости этого конденсатора со знаком минус. Далее записываются проводимости ветвей между двумя узлами (между котоыми есть элемент с проводимостью) со знаком минус  например проводимость ветви между узлами 1 и 2 записывается G12 или G21 равна проводимости резистора R3 со знаком минус. Для узлов к которым подсоединены ветви с источниками напряжения записываются переменные с номерами соответствующих узлов. В данном случае когда все источники одним концом подсоединены к нулевому узлу (земле) который не считается имеющимся переменным J1, J2, J5, J8 присваивается отношение напряжения источника к сопротивлению резистора в ветви с источником со знаком плюс если ток направлен к узлу и со знаком минус если наоборот. Для узла к которому подсоединён источник Е1 и не обозначенного на рисунке применён перенос источников ЭДС (на рисунке не показано, оставлена первоначальная схема).
   

Создаются две матрицы первая с чслом столбцов и строк равным числу узлов, вторая с числом строк равным числу узлов. В первую матрицу на главную диагональ записываются переменные G11-G88. В остальные ячейки записываются проводимости между узлами номера которых соответствуют номеру столбца и номеру строки матрицы как в примере ниже. Первая матрица должна получиься симметричной относительно главной диагонали если в неё подставить численные значения проводимостей. Во вторую матрицу в строки с номерами узлов к которым подсоединены источники напряжения соответственно записываются переменные J1, J2, J5, J8.
В не занятые  ячейки матриц записываются нули.

Умножив обращённую матрицу G на матрицу J получим матрицу потенциалов узлов с первого по восьмой. Перемножать матрицы можно только в таком порядке как показано на примере иначе маткад выведет ошибку. Для обращения к элементам матрицы U можно использовать нижний индекс. Функцией Re находится действительная часть числа, функцией Im мнимая.

Теперь можно найти требуемые токи и их действующие значения. Действующее значение тока находится как корень квадратный из суммы квадратов действительной и мнимой составляющей значения тока.

В маткаде существует возможность расчёта по системе уравнений без использования матриц, такой расчёт (для метода контурных токов) рассмотрен в статье Расчёт систем уравнений в маткаде, метод контурных токов. В статье расчёт схемы методом узловых потенциалов пример 2 рассмотрен более подробно более простой пример расчёта схемы методом узловых потенциалов.