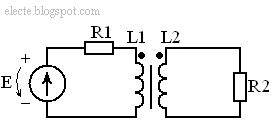
Электрические схемы могут иметь индуктивно связанные катушки. Такие схемы могут быть рассчитаны методом уравнений Кирхгофа или методом контурных токов. Индуктивно связанными катушками могут быть например обмотки трансформатора. Рассмотрим схему на рисунке 1:
В этой схеме нет узлов поэтому метод узловых потенциалов к ней не применим. L1 и L2 это индуктивно связанные катушки. Для расчёта схемы выберем направления токов в ветвях и направления контуров:
У индуктивно связанных катушек L1 и L2 имеется взаимная индуктивность M12. Катушки в схеме включены согласно т.к. ток I1 входит в сторону катушки L1 где точка и при этом ток I2 входит сторону катушки L2 где точка. Так как в схеме нет узлов то уравнения по первому закону Кирхгофа для неё составить нельзя. Составим уравнения по второму закону Кирхгофа:
Буквой j, в данном случае, обозначается мнимая единица т.е. квадратный корень из -1. В левой части уравнения для первого контура: записано произведение тока I1 на сопротивление R1 со знаком плюс т.к. направление тока в ветви совпадает с направлением обхода контура, записано произведение тока I1 на реактивное сопротивление катушки L1 со знаком плюс т.к. направление тока в ветви совпадает с направлением обхода контура, записано произведение тока I1 на реактивное сопротивление взаимной индуктивности M12 со знаком плюс т.к. ток I1 входит в сторону катушки L1 где точка и при этом ток I2 входит сторону катушки L2 где точка. Если бы ток I1 входил в сторону катушки L1 где нет точки и при этом ток I2 входил в сторону катушки L2 где нет точки то также со знаком плюс было бы записано произведение тока I1 на реактивное сопротивление взаимной индуктивности M12, т.е. первое уравнение не изменилось бы. Если бы ток I1 входил в сторону катушки L1 где точка а ток I2 входил в сторону катушки L2 где точки нет то произведение тока I1 на реактивное сопротивление взаимной индуктивности M12 было бы записано со знаком минус. Если бы ток I1 входил в сторону катушки L1 где нет точки а ток I2 входил в сторону катушки L2 где точка то произведение тока I1 на реактивное сопротивление взаимной индуктивности M12 также было бы записано со знаком минус. В правой части уравнения для первого контура записано ЭДС E источника E со знаком плюс т.к. направление обхода первого контура совпадает с направлением ЭДС этого источника или т.к. напряжение на этом источнике не совпадает с направлением обхода контура поэтому E могло быть записано в левую часть со знаком минус или в правую часть со знаком плюс. Аналогично составлено второе уравнение для второго контура. Преобразуем систему уравнений (1) к виду:
Запишем систему уравнений (2) в матричном виде:
Пусть:
E=10 (ЭДС переменная)(и мнимая часть=0),
f=50Гц (частота синусоидального напряжения E на источнике ЭДС E),
R1=2,
R2=2,
L1=0.01,
L2=0.01,
k=0.5 -коэффициент связи катушек L1 и L2.
Коэффициент связи k показывает какая часть магнитного потока первой катушки пронизывает вторую катушку (и наоборот). Коэффициент связи k может принимать значения в диапазоне от 0 до 1. Если k=0.5 то 50% потока первой катушки пронизывает вторую и наоборот. Рассчитаем взаимную индуктивность M12 и циклическую частоту ω:
Рассчитаем систему уравнений (3) методом Крамера:
Деление комплексных чисел осуществляется по формуле:
Баланс мощностей составляется как для обычной схемы без взаимной индуктивности. Мощность источника:
Мощность приёмников:
Мощность выдаваемая источником равна мощности потребляемой приёмниками т.е. баланс мощностей сошёлся что свидетельствует о правильности расчёт схемы.
Рисунок 1 - Схема с индуктивно связанными катушками
В этой схеме нет узлов поэтому метод узловых потенциалов к ней не применим. L1 и L2 это индуктивно связанные катушки. Для расчёта схемы выберем направления токов в ветвях и направления контуров:
Рисунок 2 - Схема с вспомогательными обозначениями
Буквой j, в данном случае, обозначается мнимая единица т.е. квадратный корень из -1. В левой части уравнения для первого контура: записано произведение тока I1 на сопротивление R1 со знаком плюс т.к. направление тока в ветви совпадает с направлением обхода контура, записано произведение тока I1 на реактивное сопротивление катушки L1 со знаком плюс т.к. направление тока в ветви совпадает с направлением обхода контура, записано произведение тока I1 на реактивное сопротивление взаимной индуктивности M12 со знаком плюс т.к. ток I1 входит в сторону катушки L1 где точка и при этом ток I2 входит сторону катушки L2 где точка. Если бы ток I1 входил в сторону катушки L1 где нет точки и при этом ток I2 входил в сторону катушки L2 где нет точки то также со знаком плюс было бы записано произведение тока I1 на реактивное сопротивление взаимной индуктивности M12, т.е. первое уравнение не изменилось бы. Если бы ток I1 входил в сторону катушки L1 где точка а ток I2 входил в сторону катушки L2 где точки нет то произведение тока I1 на реактивное сопротивление взаимной индуктивности M12 было бы записано со знаком минус. Если бы ток I1 входил в сторону катушки L1 где нет точки а ток I2 входил в сторону катушки L2 где точка то произведение тока I1 на реактивное сопротивление взаимной индуктивности M12 также было бы записано со знаком минус. В правой части уравнения для первого контура записано ЭДС E источника E со знаком плюс т.к. направление обхода первого контура совпадает с направлением ЭДС этого источника или т.к. напряжение на этом источнике не совпадает с направлением обхода контура поэтому E могло быть записано в левую часть со знаком минус или в правую часть со знаком плюс. Аналогично составлено второе уравнение для второго контура. Преобразуем систему уравнений (1) к виду:
Запишем систему уравнений (2) в матричном виде:
Пусть:
E=10 (ЭДС переменная)(и мнимая часть=0),
f=50Гц (частота синусоидального напряжения E на источнике ЭДС E),
R1=2,
R2=2,
L1=0.01,
L2=0.01,
k=0.5 -коэффициент связи катушек L1 и L2.
Коэффициент связи k показывает какая часть магнитного потока первой катушки пронизывает вторую катушку (и наоборот). Коэффициент связи k может принимать значения в диапазоне от 0 до 1. Если k=0.5 то 50% потока первой катушки пронизывает вторую и наоборот. Рассчитаем взаимную индуктивность M12 и циклическую частоту ω:
Рассчитаем систему уравнений (3) методом Крамера:
Деление комплексных чисел осуществляется по формуле:
Баланс мощностей составляется как для обычной схемы без взаимной индуктивности. Мощность источника:
Мощность приёмников:
Мощность выдаваемая источником равна мощности потребляемой приёмниками т.е. баланс мощностей сошёлся что свидетельствует о правильности расчёт схемы.

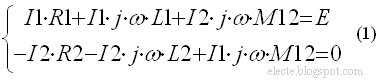


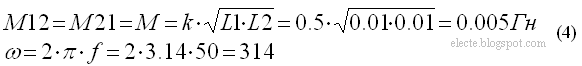




Комментариев нет:
Отправить комментарий