Если имеется схема с известными: сопротивлениями резисторов, ЭДС источников ЭДС и токами источников тока и надо рассчитать токи во всех ветвях, этой схемы, то можно воспользоваться каким либо методом расчёта схем, например методом уравнений Кирхгофа который является самым универсальным и подходит для расчёта любых схем. Для проверки правильности расчёта схемы: рассчитывается мощность потребляемая в схеме Pпр (мощность приёмников), рассчитывается мощность вырабатываемая в этой схеме Pист (мощность источников) после чего эти две рассчитанные мощности сравниваются, если они равны (м.б. с некоторой погрешностью (т.е. различаются но чуть чуть)) то баланс мощностей сошёлся и решение считается верным, если не равны то схема пересчитывается. Рассмотрим схему на рисунке 1:
В этой схеме есть: 4 резистора R1, R2 ,R3, R4 с сопротивлениями равными R1, R2, R3, R4 (немного неграмотно параметры элементов обозначать также как и сами элементы но так бывает удобней); источник тока J с током равным J и источник ЭДС с напряжением на нём равным по модулю его ЭДС равным E и напряжение на этом источнике противоположно по направлению ЭДС этого источника (направление ЭДС источника ЭДС на схемах указывается внутри этого источника а направление напряжения на нём указывается снаружи). На самом деле источник ЭДС создаёт только ЭДС а напряжение при этом существует на части (имеющей сопротивление) контура подключенной к этому источнику но бывает удобно составлять правильные уравнения считая что существуют напряжения на источниках ЭДС и напряжения на других элементах а ЭДС не учитывать. Для того чтобы рассчитать схему на рисунке 1 пронумеруем в ней узлы (начиная с нуля), выберем направления токов во всех ветвях (можно произвольно), выберем независимые контуры (желательно (для метода контурных токов) в одну сторону и так чтобы они не пересекали ветви на рисунке):
Уравнения по первому закону (правилу) Кирхгофа составляются для узлов начиная с первого (т.е. для нулевого узла уравнение по первому закону (правилу) Кирхгофа можно не составлять а для остальных надо). Нулевым узлом можно выбрать любой а все остальные нумеровать по всякому. Уравнения по второму закону (правилу) Кирхгофа составляются для контуров (в количестве = количество ветвей - количество узлов + 1) в которых нет источника тока и есть хотя бы одна ветвь которая не принадлежит другим контурам а для расчёта.
Перенеся в правую часть уравнений токи источников тока и напряжения источников ЭДС можно (а можно в принципе и не переносить) решить систему уравнений и получить токи I1-I4. Но в данном случае можно применить более простые методы нахождения токов нежели метод уравнений Кирхгофа. Например можно использовать метод контурных токов. Уравнения методом контурных токов можно составлять в матричном виде, для схемы на рисунке 2:
Далее если все (даже вспомогательные с источниками тока) контуры направлены в одну сторону и контуры не пересекают ветви на рисунке.
На главной диагонали квадратной матрицы (которая слева) ставятся суммы сопротивлений резисторов входящих в соответствующие контуры, например в ячейке в первой строке и первом столбце ставиться сумма сопротивлений резисторов первого контура (контур I11 с контурным током I11), в ячейке во второй строке и втором столбце ставится сумма сопротивлений второго контура I22 (контур I22 с контурным током I22) и т.д. В остальных ячейках этой матрицы ставятся со знаком минус сопротивления резисторов общих для двух каких либо контуров, например если у первого и второго контура общий резистор с сопротивлением R3 (см. рисунок 2) то -R3 записывается в ячейку в первой строке и втором столбце и также записывается в ячейку во втором столбце и первой строке. Матрица с сопротивлениями умножается на матрицу контурных токов. В правой части уравнения (2) находится матрица источников. В первой строке матрицы источников находится произведение тока источника тока J на сопротивление резистора R1 со знаком плюс. Для того чтобы это записать был выбран дополнительный контур направление которого совпадает с направлением тока источника тока, это произведение записывается со знаком плюс т.к. иначе оно могло быть записано в левой части со знаком минус потому что в левой части со знаком плюс могут быть только суммы сопротивлений контуров без источников токов, но это только при том что все контуры направлены в одну сторону и не пересекают ветви на рисунке. R1 - это резистор общий для первого контура и контура с источником тока. Если бы источник тока был направлен в другую сторону то направление контурного тока J следовало бы выбрать в другую сторону и тогда бы в первой строке матрицы источников стояло произведение J*R1 со знаком минус т.к. контур J был бы направлен через ветвь с резистором R1 в ту же сторону что и контур I11.
Во второй строке матрицы источников находится ЭДС источника ЭДС со знаком минус т.к. эта ЭДС направлена противоположно току (с выбранным направлением) в ветви. Уравнения этим методом можно было составить применяя другой подход.
Контурные токи I11 и I22 находятся при решении уравнения (2). Токи находятся по формулам:
Для ветви с током I1 ток I1=J-I11 т.к. контуру J принадлежит эта ветвь и направление этого контура совпадает с током I1 поэтому J со знаком плюс, контуру I11 принадлежит эта ветвь и направление этого контура не совпадает с током I1 поэтому I11 со знаком минус. Контуру I11 принадлежит только одна ветвь с током I2 и направление этого тока совпадает с направлением контура I11 поэтому I2=+I11. Для других токов аналогично.
Для нахождения токов можно (если нет ветвей с одним источником ЭДС без резистора (или др. элемента с сопротивлением)) также использовать метод узловых потенциалов:
На главной диагонали квадратной матрицы ставятся суммы проводимостей ветвей присоединённых к соответствующим узлам, например в ячейке на первой строке в первом столбце стоит сумма проводимостей присоединённых к первому узлу. К первому узлу присоединено три ветви проводимость ветви с источником тока равна нулю поэтому она не записывается, проводимость ветви с резистором R1 равна 1/R1 (т.к. проводимость - величина обратная сопротивлению), проводимость ветви с резистором R2 равна 1/R2. В ячейке на второй строке во втором столбце записана сумма проводимостей присоединённых ко второму узлу. В остальных ячейках этой матрицы ставятся со знаком минус проводимости ветвей между двумя какими либо узлами кроме нулевого. Проводимость между первым и вторым узлами равна 1/R2 поэтому в ячейке на второй строке и первом столбце ставится -1/R2 и в ячейке на первой строке и втором столбце ставиться -1/R2. Если между узлами нет проводимости то в соответствующую ячейку ставиться ноль. Метод контурных токов и метод узловых потенциалов имеют сходство. Матрица с проводимостями умножается на матрицу с потенциалами узлов. В правой части уравнения (4) стоит одностолбцовая матрица источников. Первая строка матрицы источников соответствует первому узлу, вторая второму и т.д. В первую строку матрицы источников вписывается ток J источника тока J со знаком плюс т.к. ток J источника J направлен к первому узлу (если от то со знаком "-"). Во вторую строку матрицы источников вписано произведение ЭДС E источника ЭДС E на проводимость ветви с этим источником ЭДС со знаком плюс т.к. эта ЭДС направлена ко второму узлу (если от то со знаком "-"). Если к узлу подсоединено несколько источников то все они с соответствующими знаками записываются в соответствующую этому узлу строку. Потенциалы узлов находятся при решении уравнения (4). Токи находятся по формулам:
I1=φ1/R1 т.к. ток на резисторе R1 равен отношению напряжения, на этом резисторе, к сопротивлению этого резистора а напряжение на этом резисторе равно разности потенциалов на этом резисторе, т.к. ток I1 направлен (направление выбранное) от узла 1 к узлу 0 то напряжение на этом резисторе с учётом направления тока находится вычитанием потенциала узла 0 из потенциала узла 1, т.к. потенциал узла 0 равен нулю то он не пишется и получается что напряжение на резисторе R1 с учётом направления тока равно φ1. I4=(E-φ2)/R4 т.к. ток на резисторе R4 равен отношению напряжения, на этом резисторе, к сопротивлению этого резистора а напряжение на этом резисторе равно E-(φ2-φ0) по второму закону Кирхгофа.
Для примера решим уравнение (2) и примем например что:
J=1
R1=1
R2=1
R3=1
R4=1
E=1
Решить его можно например методом Крамера. Для решения методом Крамера найдём определитель (детерминант) матрицы с сопротивлениями:
Найдём определитель матрицы с сопротивлениями у которой первый столбец заменён на столбец матрицы источников:
Найдём определитель матрицы с сопротивлениями у которой второй столбец заменён на столбец матрицы источников:
Найдём контурные токи:
Найдём токи:
Для проверки правильности расчёта схемы (нахождения токов) рассчитаем мощность потребляемую приёмниками энергии (ими м.б. резисторы или источники (в данном случае только резисторы)):
Мощность (потребителей и источников) равна произведению тока протекающего через элемент (потребитель или источник) на напряжение на нём. Ток в квадрате это ток умноженный на ток, если ток умножить на сопротивление то получиться напряжение поэтому например (I1^2)*R1 это мощность потребляемая резистором R1.
Для резисторов все мощности со знаком плюс, направления токов не учитываются.
Рассчитаем мощность выдаваемую источниками:
Если напряжение на ветви с источником тока направлено согласно току (направление которого указано стрелками в источнике) источника тока то мощность источника тока была бы записана в уравнение (12) со знаком минус и тогда предполагалось бы что источник потребляет энергию или эта мощность была бы записана в уравнение (11) со знаком плюс. Если бы ЭДС источника была направлена в направлении противоположном току (направление которого выбрано и показано на рисунке 2 стрелкой) в этой ветви то мощность этого источника была бы записана в уравнение (12) со знаком минус или в уравнение (11) со знаком плюс. Знаки мощностей записываемых в уравнения для проверки определяются по выбранным в самом начале направлениям токов. Т.к. мощности источников равны мощностям приёмников то можно считать что баланс мощностей сошёлся и расчёт схемы выполнен правильно.
Для расчёта токов I1-I4 в схеме на рисунке 2 с учётом направлений токов (как на рисунке 2) можно воспользоваться программой:
Если вы заметили ошибку то напишите о ней пожалуйста в комментарии
Рисунок 1 - Схема
Рисунок 2 - Схема с вспомогательными обозначениями
Уравнения по первому закону (правилу) Кирхгофа составляются для узлов начиная с первого (т.е. для нулевого узла уравнение по первому закону (правилу) Кирхгофа можно не составлять а для остальных надо). Нулевым узлом можно выбрать любой а все остальные нумеровать по всякому. Уравнения по второму закону (правилу) Кирхгофа составляются для контуров (в количестве = количество ветвей - количество узлов + 1) в которых нет источника тока и есть хотя бы одна ветвь которая не принадлежит другим контурам а для расчёта.
На главной диагонали квадратной матрицы (которая слева) ставятся суммы сопротивлений резисторов входящих в соответствующие контуры, например в ячейке в первой строке и первом столбце ставиться сумма сопротивлений резисторов первого контура (контур I11 с контурным током I11), в ячейке во второй строке и втором столбце ставится сумма сопротивлений второго контура I22 (контур I22 с контурным током I22) и т.д. В остальных ячейках этой матрицы ставятся со знаком минус сопротивления резисторов общих для двух каких либо контуров, например если у первого и второго контура общий резистор с сопротивлением R3 (см. рисунок 2) то -R3 записывается в ячейку в первой строке и втором столбце и также записывается в ячейку во втором столбце и первой строке. Матрица с сопротивлениями умножается на матрицу контурных токов. В правой части уравнения (2) находится матрица источников. В первой строке матрицы источников находится произведение тока источника тока J на сопротивление резистора R1 со знаком плюс. Для того чтобы это записать был выбран дополнительный контур направление которого совпадает с направлением тока источника тока, это произведение записывается со знаком плюс т.к. иначе оно могло быть записано в левой части со знаком минус потому что в левой части со знаком плюс могут быть только суммы сопротивлений контуров без источников токов, но это только при том что все контуры направлены в одну сторону и не пересекают ветви на рисунке. R1 - это резистор общий для первого контура и контура с источником тока. Если бы источник тока был направлен в другую сторону то направление контурного тока J следовало бы выбрать в другую сторону и тогда бы в первой строке матрицы источников стояло произведение J*R1 со знаком минус т.к. контур J был бы направлен через ветвь с резистором R1 в ту же сторону что и контур I11.
Во второй строке матрицы источников находится ЭДС источника ЭДС со знаком минус т.к. эта ЭДС направлена противоположно току (с выбранным направлением) в ветви. Уравнения этим методом можно было составить применяя другой подход.
Контурные токи I11 и I22 находятся при решении уравнения (2). Токи находятся по формулам:
Для нахождения токов можно (если нет ветвей с одним источником ЭДС без резистора (или др. элемента с сопротивлением)) также использовать метод узловых потенциалов:
Для примера решим уравнение (2) и примем например что:
J=1
R1=1
R2=1
R3=1
R4=1
E=1
Решить его можно например методом Крамера. Для решения методом Крамера найдём определитель (детерминант) матрицы с сопротивлениями:
Для резисторов все мощности со знаком плюс, направления токов не учитываются.
Рассчитаем мощность выдаваемую источниками:
Для расчёта токов I1-I4 в схеме на рисунке 2 с учётом направлений токов (как на рисунке 2) можно воспользоваться программой:
Если вы заметили ошибку то напишите о ней пожалуйста в комментарии
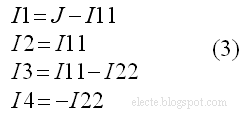
Неправильно программа считает. Подставил полученные значения токов в Вашу формулу для расчета потребляемой мощности и не получил тот ответ, которые программа выдала.
ОтветитьУдалить