Рассмотрим формирование математической модели для анализа переходного процесса в схеме на рисунке 1:
Рисунок 1 - Схема
Для схемы на рисунке 1 составим направленный граф и выделим на нем нормальное дерево:
Рисунок 2 - Направленный граф
Дерево графа показано жирными линиями. Хорды графа показаны тонкими серыми линиями. Граф показывает связи между узлами которые (связи) называются ветвями графа, направленный граф, помимо этого, показывает направления ветвей. В данном случае для каждого элемента поставлена отдельная ветвь. Все узлы находятся в местах соединения ветвей. Дерево графа это набор ветвей образующий путь между всеми узлами но не образующий замкнутых контуров. Выбор ветвей дерева должен производиться с учётом следующего приоритета:
1) источники ЭДС,
2) конденсаторы,
3) резисторы,
4) катушки.
Ветви не вошедшие в дерево являются хордами. Хорды выбираются в соответствии с приоритетом:
1) конденсаторы,
2) резисторы,
3) катушки,
4) источники тока.
Далее выбираются контуры так чтобы в каждом из них содержалась одна хорда и направление обхода контура выбирается по направлению этой хорды.
1) конденсаторы,
2) резисторы,
3) катушки,
4) источники тока.
Далее выбираются контуры так чтобы в каждом из них содержалась одна хорда и направление обхода контура выбирается по направлению этой хорды.
Математическая модель цепи может быть найдена из уравнения 1:
Где Ip - матрица токов ребер, Ux - матрица напряжений хорд, F- матрица ребер, Up - матрица напряжений ребер, Ix - матрица токов хорд.
Запишем матрицу токов ребер и матрицу токов хорд в соответствии с приведенными выше приоритетами для ребер и для хорд:
IE - ток источника, второй элемент матрицы Ip это ток конденсатора (смотри формулу 2 в статье "ёмкостное сопротивление конденсатора"), IRE - ток резистора RE, IRL - ток резистора RL, IRH - ток резистора RH, IL - ток катушки.
Запишем матрицу напряжений ребер и матрицу напряжений хорд в соответствии с приведенными выше приоритетами для ребер и для хорд:
E - ЭДС источника E, UC - напряжение конденсатора, последние два элемента матрицы Up и первый элемент матрицы Ux - напряжения соответствующих резисторов (из закона Ома), последний элемент матрицы Ux это напряжение катушки (смотри "первый закон коммутации, ЭДС катушки"). Далее составим матрицу контуров B:
Число строк матрицы контуров равно числу контуров (в нашем случае два), число столбцов матрицы контуров равно числу ветвей. Каждый столбец принадлежит какой либо ветви а каждая строка - какому либо контуру, каждый контур принадлежит какой либо хорде. Столбцы и строки выставляются по порядку в соответствии с приведенными выше приоритетами для ребер и для хорд. Матрица контуров B заполняется так:
- Если ветвь принадлежит какому то контуру и совпадает с ним по направлению то в ячейке столбец которой принадлежит этой ветви а строка принадлежит этому контуру записывается 1.
- Если ветвь принадлежит какому то контуру и не совпадает с ним по направлению то в ячейке столбец которой принадлежит этой ветви а строка принадлежит этому контуру записывается -1.
- Если ветвь не принадлежит какому то контуру то в ячейке столбец которой принадлежит этой ветви а строка принадлежит этому контуру записывается 0.
Например ветвь E принадлежит контуру II и не совпадает с ним по направлению поэтому в ячейке столбца принадлежащего ветви E (первый столбец) и строки принадлежащей контуру II (вторая строка) записывается -1. Та часть матрицы столбцы которой принадлежат
ветвям-ребрам называется матрицей ребер, остальная часть матрицы называется матрицей хорд. Если на главной диагонали матрицы хорд стоят единицы а в остальной её части - нули (как в нашем случае) то из матрицы контуров B можно выделить матрицу ребер F если нет то значит при составлении графа и/или при составлении матрицы контуров B была допущена ошибка. Контуры графа нумеруются согласно второму приоритету и их принадлежности хордам.
Выделим матрицу ребер F из матрицы контуров B:
Найдем матрицу -F:
Транспонируем матрицу F (заменим столбцы строками а строки столбцами):
Подставим найденные матрицы Ip, Ux, -F, FT, Up, Ix в уравнение 1:
Перемножим матрицы во второй части уравнения:
Запишем это выражение в виде системы уравнений:
Из второго уравнения выразим производную напряжения конденсатора по времени через напряжение конденсатора используя пятое уравнение а из шестого уравнения выразим производную тока катушки по времени через ток катушки используя первое, третье и четвёртое уравнения:
Данная система уравнений представляет собой математическую модель схемы на рисунке 1.
Перемножим матрицы во второй части уравнения:
Запишем это выражение в виде системы уравнений:
Из второго уравнения выразим производную напряжения конденсатора по времени через напряжение конденсатора используя пятое уравнение а из шестого уравнения выразим производную тока катушки по времени через ток катушки используя первое, третье и четвёртое уравнения:








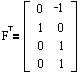


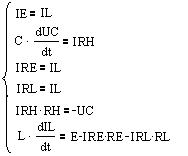

Комментариев нет:
Отправить комментарий