На рисунке 1 представлена однослойная катушка: имеющая круглое сечение, не имеющая сердечника (магнитная проницаемость равна единице), длинной l=0.01м, диаметром d=0.01м, числом витков w=3:
Рисунок 1 - Катушка
Индуктивность - это коэффициент связывающий ток (силу тока) I протекающий по виткам катушки и её потокосцепление, математически это можно представить в виде формулы (1):
Из (1) можно выразить индуктивность:
Формула для расчёта потокосцепления катушки была выведена в статье "расчёт потокосцепления однослойной катушки", там же есть программа для его расчёта (программа использует равенство (3)).
В знаменателе формулы (3) длинна l.
Подставим (3) в (2) и получим формулу для расчёта индуктивности, для данного случая:
Подставим (3) в (2) и получим формулу для расчёта индуктивности, для данного случая:
Так как сечение круглое и известен диаметр d то площадь можно найти по формуле:
Диаметр берется средний.
Подставим найденную площадь S; известные: число витков w, длину l, магнитную проницаемость материала сердечника, магнитную проницаемость вакуума в (4) и найдем индуктивность для нашего примера (рисунок 1):
Подставим найденную площадь S; известные: число витков w, длину l, магнитную проницаемость материала сердечника, магнитную проницаемость вакуума в (4) и найдем индуктивность для нашего примера (рисунок 1):
Для расчёта индуктивности можно воспользоваться программой приведенной ниже:
Если программа не работает то скопируйте её html код в блокнот и сохраните в формате html.
Если страница открыта в Internet Explorer то для работы программы может понадобиться "разрешить заблокированное содержимое".
Если число слоёв катушки не велико (несколько слоёв) а диаметр провода мал по отношению к её размерам то можно воспользоваться формулой (4) и получить приближенный результат. Необходимо учитывать что форма катушки может быть такой что результат расчёта её индуктивности по формуле (4) может быть очень неточным.
Если программа не работает то скопируйте её html код в блокнот и сохраните в формате html.
Если страница открыта в Internet Explorer то для работы программы может понадобиться "разрешить заблокированное содержимое".
Если число слоёв катушки не велико (несколько слоёв) а диаметр провода мал по отношению к её размерам то можно воспользоваться формулой (4) и получить приближенный результат. Необходимо учитывать что форма катушки может быть такой что результат расчёта её индуктивности по формуле (4) может быть очень неточным.






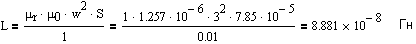
Спасибо!
ОтветитьУдалитьОчень полезная программа.
Жалъ, что толко на соленоида. Я иногда потребовал бы и разчёт тороида.
В интернете полно формул для расчета индуктивностей
ОтветитьУдалитьдлинна)))
ОтветитьУдалить